https://quick-bench.com/
9. Optimization#
First of all :
“Programmers waste enormous amounts of time thinking about, or worrying about, the speed of noncritical parts of their programs, and these attempts at efficiency actually have a strong negative impact when debugging and maintenance are considered. We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%.” - Donald Knuth
First, make your program correct, then measure, then optimize. Optimization can be achieved by just using compiler flags, by using already optimized libraries, and sometimes by being careful with our memory usage. Some low level techniques are better left to the compiler.
Some tips: https://news.ycombinator.com/item?id=39564632
9.1. Compiler flags#
See : https://gcc.gnu.org/onlinedocs/gcc/Optimize-Options.html
Some warnings:
Optimizations enabled by -ffast-math: https://kristerw.github.io/2021/10/19/fast-math/
Beware of fast-math: https://simonbyrne.github.io/notes/fastmath/
Beware of fast-math (Hackernews discussion): https://news.ycombinator.com/item?id=29201473
Sometimes just using compiler optimization flags with can improve dramatically our code performance. Normally, you want to run your code through several compiler flags to check for speed ups but also for possible uncovered bugs.
Compile without (-O0) and with optimization (-O3) the following code
and compare their runtime (this is a very old c-based code but still works):
// Credits : Ivan Pulido
/* Shows a way to do operations that require a specific order (e.g.,
* transpositions) while avoiding cache misses. */
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define min( a, b ) ( ((a) < (b)) ? (a) : (b) )
int main(){
const int n = 512;
const int csize = 32;
float ***a, ***b;
clock_t cputime1, cputime2;
int i,j,k,ii,jj,kk;
// Allocating memory for array/matrix
a = malloc(n*sizeof(float **));
for (i=0; i<n; i++){
a[i] = malloc(n*sizeof(float*));
for (j=0; j<n; j++)
a[i][j] = malloc(n*sizeof(float));
}
b = malloc(n*sizeof(float **));
for (i=0; i<n; i++){
b[i] = malloc(n*sizeof(float*));
for (j=0; j<n; j++)
b[i][j] = malloc(n*sizeof(float));
}
// Filling matrices with zeros
for(i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
a[i][j][k] = 0;
for(i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
b[i][j][k] = 0;
// Direct (inefficient) transposition
cputime1 = clock();
for (i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
a[i][j][k] = b[k][j][i];
cputime2 = clock() - cputime1;
printf("Time for transposition: %f\n", ((double)cputime2)/CLOCKS_PER_SEC);
// Transposition using cache-blocking
cputime1 = clock();
for (ii=0; ii<n; ii+=csize)
for (jj=0; jj<n; jj+=csize)
for (kk=0; kk<n; kk+=csize)
for (i=ii; i<min(n,ii+csize-1); ++i)
for (j=jj; j<min(n,jj+csize-1); ++j)
for (k=kk; k<min(n,kk+csize-1); ++k)
a[i][j][k] = b[k][j][i];
cputime2 = clock() - cputime1;
printf("Time for transposition: %f\n", ((double)cputime2)/CLOCKS_PER_SEC);
return 0;
}
When you compile without optimization and execute, you will get something like
gcc -O0 cache_blocking.c
./a.out
But, if you use optimization, you can get an important improvement
gcc -O2 cache_blocking.c
./a.out
Actually we can compare all optimization levels to check their impact:
for level in 0 1 2 3; do echo "level: $level"; gcc -O$level cache_blocking.c; ./a.out; done
Be careful when using -O3: it activates some unsafe math optimizations
that will not respect IEEE754.
9.1.1. Exercise#
Vary both the matrix size and the cache size to compute both times. Plot the results on two different 3d plots (in gnuplot use splot). Repeat for -O0 and -O2
9.2. Memory layout#
The memory layout should always be taken into account since cache misses will greatly affect a program performance. Always measure with a profiler and if possible with cachegrind in order to detect possible excessive cache misses.
See Cache Nightmares: https://www.youtube.com/watch?v=xFMXIgvlgcY
The following code shows how a simple index change in a matrix operation could have a huge impact on the app performance:
// Credit Ivan Pulido
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(){
const int n = 256;
clock_t cputime1, cputime2;
float ***a;
int i,j,k;
// Allocating memory for array/matrix
a = malloc(n*sizeof(float **));
for (i=0; i<n; i++){
a[i] = malloc(n*sizeof(float*));
for (j=0; j<n; j++)
a[i][j] = malloc(n*sizeof(float));
}
cputime1 = clock();
for (k=0; k<n; ++k)
for (j=0; j<n; ++j)
for (i=0; i<n; ++i)
a[i][j][k] = 1.0;
cputime2=clock() - cputime1;
printf("Time with fast index inside: %lf\n", ((double)cputime2)/CLOCKS_PER_SEC);
cputime1 = clock();
for(i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
a[i][j][k] = 2.3;
cputime2=clock() - cputime1;
printf("Time with fast index outside: %lf\n", ((double)cputime2)/CLOCKS_PER_SEC);
// Clearing memory
for (i=0; i<n; i++){
for (j=0; j<n; j++)
free(a[i][j]);
free(a[i]);
}
free(a);
return 0;
}
gcc codes/cache_lines.c
./a.out
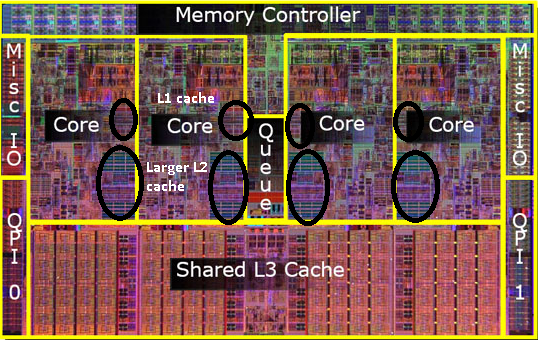
Being nice to the cache comes from the modern cpu architecture, as shown in the next figure
L1, L2 and L3 caches. Source https://medium.com/software-design/why-software-developers-should-care-about-cpu-caches-8da04355bb8a
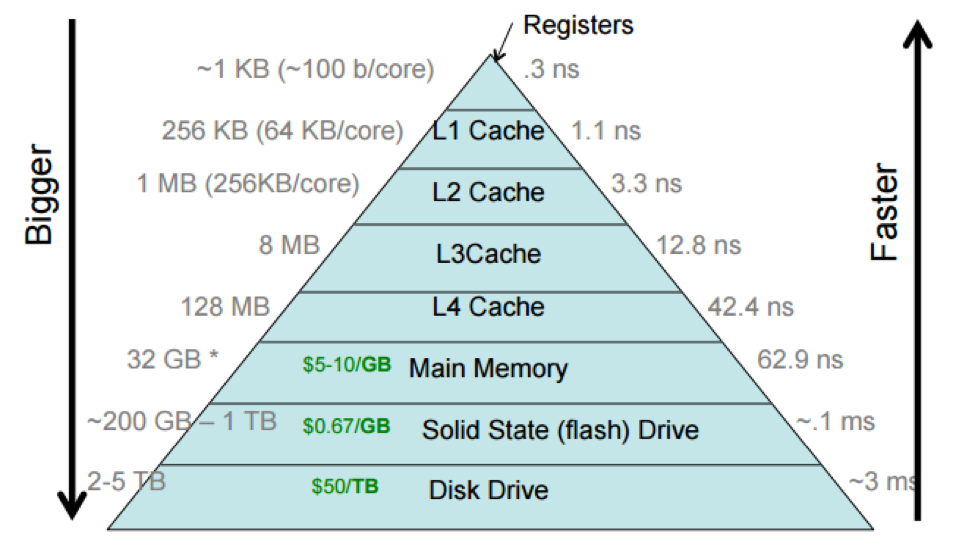
The relative bandwidth across the different cpu and momory controllers explain why it is important to have the processed data as much time as possible in the cache
Relative bandwidth across different cpu and computer parts. Credit: <https://cs.brown.edu/courses/csci1310/2020/assign/labs/lab4.html
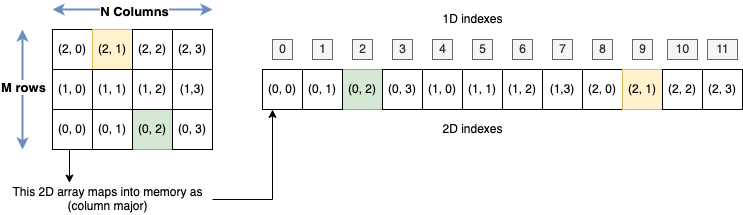
Since c/c++ store matrices in row major order, then accesing the memory in the same way will benefit the cache and therefore increases our program performance.
9.2.1. Exercise#
Vary again the matrix size. Is the time difference important for all sizes? plot it.
Explore the effect of different optimization flags
9.3. What data structures to use?#
It depends greatly from the problem. But for the typical applications of
vector and matrix computations, we can expect that homogeneous and
contiguous arrays are the data structures to go. In that case, it is
advisable to use std::vector as the go to data struct since it is as
efficient as an primitive arra, handles automatically the dynamic memory
in the heap, and plays nice with the C++ STL.
A primitive static array is limited by the stack. Play with the values of M and N in the following code until you get a seg fault just by running the code.
#include <iostream>
int main(void)
{
const int M = 7000;
const int N = 500;
double data[M][N] = {{0.0}};
std::cout << data[M/2][N/2] << std::endl;
return 0;
}
Is the maximum size related somehow with the output of the command
ulimit -s ?
To be able to use more memory, you could better use dynamic memory with
primitive arrays, but you will have to manage the new/delete parts in
your code. Check that foloowing code does not die on the same sizes as
the previous one
#include <iostream>
int main(void)
{
const int M = 7000;
const int N = 500;
double **data = nullptr;
data = new double *[M];
for (int ii = 0; ii < M; ++ii){
data[ii] = new double [N];
}
std::cout << data[M/2][N/2] << std::endl;
for (int ii = 0; ii < M; ++ii){
delete [] data[ii];
}
delete [] data;
return 0;
}
But be careful, memory obtained susing double/multiple pointers is not guaranteed to be contigous, so it is much better to just ask for a large one-dimensional array and just model the 2D shape with smart indexes
#include <iostream>
int main(void)
{
const int M = 7000;
const int N = 500;
double *data = nullptr;
data = new double [M*N];
// [id][jd] -> id*N + jd
std::cout << data[M*N/2 + N/2] << std::endl;
delete [] data;
return 0;
}
This is an example of a 2d array actually stored as a 1d array in memory:
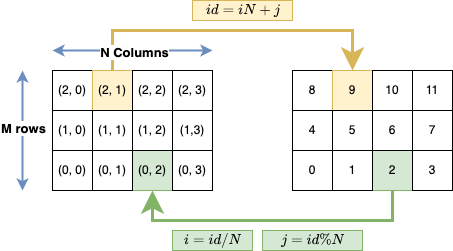
And this is the illustration of the mapping that allows us to go to/from different dimensions:
Finally, to avoid managing manually the memory, it is much better to use
std::vector,
#include <iostream>
#include <vector>
int main(void)
{
const int M = 7000;
const int N = 500;
std::vector<double> data;
data.resize(M*N);
// [id][jd] -> id*N + jd
std::cout << data[M*N/2 + N/2] << std::endl;
return 0;
}
9.3.1. Exercise#
Test the stack program to find the maximum matrix size you can use
Do the same for the last one using a vector, what is the maximum size you can reserve?
9.4. Blocking multiplication#
See https://malithjayaweera.com/2020/07/blocked-matrix-multiplication/
Blocking techniques are neat examples that show how being aware of the cache allows you to increase the performance dramatically. For instance, the following code shows a concrete example where a blocking techinque is used to compute the transpose of a matrix, with a important performance advantage:
// Credits: Ivan Pulido
/* Shows a way to do operations that require a specific order (e.g.,
* transpositions) while avoiding cache misses. */
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define min( a, b ) ( ((a) < (b)) ? (a) : (b) )
int main(){
const int n = 512;
const int csize = 32;
float ***a, ***b;
clock_t cputime1, cputime2;
int i,j,k,ii,jj,kk;
// Allocating memory for array/matrix
a = malloc(n*sizeof(float **));
for (i=0; i<n; i++){
a[i] = malloc(n*sizeof(float*));
for (j=0; j<n; j++)
a[i][j] = malloc(n*sizeof(float));
}
b = malloc(n*sizeof(float **));
for (i=0; i<n; i++){
b[i] = malloc(n*sizeof(float*));
for (j=0; j<n; j++)
b[i][j] = malloc(n*sizeof(float));
}
// Filling matrices with zeros
for(i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
a[i][j][k] = 0;
for(i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
b[i][j][k] = 0;
// Direct (inefficient) transposition
cputime1 = clock();
for (i=0; i<n; ++i)
for (j=0; j<n; ++j)
for (k=0; k<n; ++k)
a[i][j][k] = b[k][j][i];
cputime2 = clock() - cputime1;
printf("Time for transposition: %f\n", ((double)cputime2)/CLOCKS_PER_SEC);
// Transposition using cache-blocking
cputime1 = clock();
for (ii=0; ii<n; ii+=csize)
for (jj=0; jj<n; jj+=csize)
for (kk=0; kk<n; kk+=csize)
for (i=ii; i<min(n,ii+csize-1); ++i)
for (j=jj; j<min(n,jj+csize-1); ++j)
for (k=kk; k<min(n,kk+csize-1); ++k)
a[i][j][k] = b[k][j][i];
cputime2 = clock() - cputime1;
printf("Time for transposition: %f\n", ((double)cputime2)/CLOCKS_PER_SEC);
return 0;
}
Compiling and running give the following results
gcc cache_blocking.c
./a.out
The second one shows how being cache friendly really helps the performance.
9.4.1. Exercise#
Plot the time with the direct and the blocking approaches as functions of size, using
-O2. What can you conclude?
9.5. Using scientific libraries#
Scientific libraries are written by people with deep knowledge of the computer and algorithms internals , therefore saving developer time and resources. One should always try to use a established scientific library instead of writting everything from scratch. Sometimes even automatic parallelization comes for free. Examples are the Intel or AMD math libraries, the Cuda toolkit for programming on nvidia cards, and so on.
The following examples shows the time taken to transpose a matrix using a traditional approach, a blocking approach , and the eigen c++ library.
giving the following results:
Time for memory allocation: 0.315618
Time for filling: 3.607817
Time for direct transposition: 2.870691
Time for blocked transposition: 0.380954
Time for transposition with eigen: 0.031344
Time for transposition with copy in eigen: 0.310033
Time for transposition with full copy in eigen: 3.339495
-2999.9
-2999.9
15200.1
15200.1
15200.1
This shows, for instance, that eigen in some cases is not even computing the transpose but just creating an expression to access the original matrix, hence the huge speeedup and also the slow down when fully creating a copy.
9.6. Other optimization techniques#
There are other techniques sometimes applied in very speficic situations, like
Loop interchanges
Loop unrolling
for(int ii = 0; ii < n; ii++) {
array[ii] = 2*ii;
}
for(int ii = 0; ii < n; ii += 3) {
array[ii] = 2*ii;
array[ii+1] = 2*(ii+1);
array[ii+2] = 2*(ii+2);
}
Loop Fusion/Fision
Prefetching
Floating point division
Vectorization
etc
In general those techniques can applied after a careful determination that they are really needed, and sometimes the compilers already apply them at some optimization levels. Therefore it is advisable to focus on the clarity of the program first and let the compiler do its job.


