16. Introduction to MPI (distributed memory)#
16.1. Intro MPI#
MPI stands for Message Passing Interface. It is a standard which allows processes to communicate and share data across an heterogeneous setup. MPI is well suited for distributed memory systems, although it can also be used in multiprocessor environments (on those environments, OpenMP is a better suited solution). Both MPI (on any of its implementations) and OpenMP represent the most common approaches to program on a cluster environment.
NOTE: This section is heavily based on Chapter 13 of “High Performance Linux Clusters with Oscar, Rocks, OpenMosix, and MPI”, J. D. Sloan, O’Reilly.
MPI is a library of routines which allows the parts of your parallel program to communicate. But it is up to you how to split up your program/problem. There are no typical restrictions on the number of processors you can split on your problem: you can use less or more process than the number of available processors. For that reason, MPI allows you to tag every process with a given rank, on a problem of size total number of processes.
MPI can be used as a library on several languages: Fortran, C, C++ , etc. In the following, we will use mostly C.
16.2. Core MPI#
It is typical to denote the rank-0 process as the master and the remaining process (rank >= 1) as slaves. Most of the time, the slaves are processing several parts of the problem and then communicate back the results to the master. All of this is managed on a single source code which is advantageous. The following is an example of the most fundamental MPI program which constitutes a template for more complex programs:
#include "mpi.h"
#include <cstdio>
int main(int argc, char **argv)
{
int processId; /* rank of process */
int noProcesses; /* number of processes */
MPI_Init(&argc, &argv); /* Mandatory */
MPI_Comm_size(MPI_COMM_WORLD, &noProcesses);
MPI_Comm_rank(MPI_COMM_WORLD, &processId);
std::fprintf(stdout, "Hello from process %d of %d\n", processId, noProcesses);
MPI_Finalize(); /* Mandatory */
return 0;
}
Before compiling and running, we will explain the code. First of all,
the MPI functions are added by the inclusion of the mpi.h header. The
two mandatory functions MPI_Init and MPI_Finalize, must be always
present. They set-up and destroy the MPI running environment. The other
two, MPI_Comm_size and MPI_Comm_rank allows to identify the size of
the problem (number of processes) and the rank of the current process.
This allows to distinguish the master from the slaves and to split the
problem.
MPIInit
This function call must occur before any other MPI function call.
This function initializes the MPI session. It receives the argc and argv
arguments, as shown, which allows the program to read command line
arguments.
MPIFinalize
This function releases the MPI environment. This should be the last call
to MPI in the program, after all communications have ended. Your code
must be written in such a way that all processes call this function.
MPICommsize
This function returns the total number of processes running on a
communicator. A communicator is the communication group used by the
processes. The default communicator is MPI_COMM_WORLD. You can create
your own communicators to isolate several sub-groups of processes.
MPICommrank
Returns the actual rank of the calling process, inside the communicator
group. The range goes from 0 to the the size minus 1.
16.2.1. MPIGetprocessorname#
This retrieves the hostname of the current and is very useful for debugging purposes. The following example shows how to get the node name
#include "mpi.h"
#include <cstdio>
int main(int argc, char **argv)
{
int processId; /* rank of process */
int noProcesses; /* number of processes */
int nameSize; /* lenght of name */
char computerName[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv); /* Mandatory */
MPI_Comm_size(MPI_COMM_WORLD, &noProcesses);
MPI_Comm_rank(MPI_COMM_WORLD, &processId);
MPI_Get_processor_name(computerName, &nameSize);
fprintf(stderr, "Hello from process %d of %d, on %s\n", processId, noProcesses, computerName);
MPI_Finalize(); /* Mandatory */
return 0;
}
16.2.2. Compiling and running the MPI program#
Compilation can be done directly with the gcc compiler by using the
appropriate flags. But there is a helper command ready to help you:
mpicc. Save the previous example code into a file (here called
mpi-V1.c) and run the following command
$ mpicc mpi-V1.c -o hello.x
If you run the command as usual, it will expand to the number of local cores and run locally only (for example, ina two cores system):
$ ./hello.x
Hello from process 0 of 2, on iluvatarMacBookPro.local
Hello from process 1 of 2, on iluvatarMacBookPro.local
But, there is another utility which allows you to specify several parameters, like the number of processes to span, among others:
$ mpirun -np 5 ./hello.x
Hello from process 3 of 5, on iluvatarMacBookPro.local
Hello from process 1 of 5, on iluvatarMacBookPro.local
Hello from process 4 of 5, on iluvatarMacBookPro.local
Hello from process 0 of 5, on iluvatarMacBookPro.local
Hello from process 2 of 5, on iluvatarMacBookPro.local
Exercise: Print the output sorted.
16.2.3. Running an mpi on several machines#
You can run an mpi process on the same machine or in several machines, as follows
$ mpirun -np 4 -host host01,host02 ./a.out
where host01, etc is the hostname where you want to run the process.
You will need to have access by ssh to those hosts, and preferable, a
password-less setup . See also
the manual for mpirun .
You can specify a machine file for mpi tu use them and run the command with given resources. An example machine files is as follows
hostname1 slots=2
hostname2 slots=4
hostname3 slots=6
where hostname is the ip or the hostname of a given machine and the slots indicates how many jobs to run. You will need to have a passwordless access or similar to those computers.
To configure the passwordless ssh, you can follow the many tutorials online, which basically are the following steps
Generate the rsa key
ssh-keygen -t rsa
Do not set ay passphrase, just press enter.
Copy the id to the computer where you want to run processes remotely,
ssh-copy-id 192.168.10.16
Enter your password for the last time. If everything goes ok, test that you can login remotely without password by runnung
ssh 192.168.10.16
Now you can run the process remotely:
mpirun -np 100 -host 192.168.10.15,192.168.10.16 --oversubscribe ./a.out
16.3. Application: Numerical Integration (Send and Recv functions)#
To improve our understanding of MPI, and to introduce new functions, we will use a familiar problem to investigate: the computation of the area under a curve. Its easiness and familiarity allows to focus on MPI and its usage. Let’s introduce first the serial version.
16.3.1. Serial implementation of the numerical integration by rectangles#
#include <cstdio>
/* Problem parameters */
double f(double x);
double integral_serial(double xmin, double xmax, double n);
int main(int argc, char **argv)
{
const int numberRects = 50;
const double lowerLimit = 2.0;
const double upperLimit = 5.0;
double integral = integral_serial(lowerLimit, upperLimit, numberRects);
printf("The area from %lf to %lf is : %lf\n", lowerLimit, upperLimit, integral);
return 0;
}
double f(double x) {
return x*x;
}
double integral_serial(double xmin, double xmax, double n)
{
double area = 0.0;
double width = (xmax - xmin)/n;
for (int i = 0; i < n; ++i) {
double at = xmin + i*width + width/2.0; // center in the middle
double heigth = f(at);
area = area + width*heigth;
}
return area;
}
Compile and run it :
$ g++ serial_integral.cpp
$ ./a.out
The area from 2.000000 to 5.000000 is : 38.999100
Now let’s implement an mpi solution.
16.3.2. MPI solution: Point to point communication with MPISend and MPIRecv#
Check: https://mpitutorial.com/tutorials/mpi-send-and-receive/
This is an embarrassingly parallel problem. There are no data
dependencies. We can partition the domain, performing partial sums per
process, and then cumulate all of them. Basically, we will use
MPI_Comm_rank and MPI_Comm_size to partition the problem, and we
will introduce two new functions: MPI_Send, to send data, and
MPI_Recv, to receive data. These are known as blocking, point-to-point
communications.
Before checking the code, please work in groups to deduce the right problem partition (keeping the same number of inteervals per process) and how to communicate data. Use a shared whiteboard, like google jamboard.
#include "mpi.h"
#include <cstdio>
#include <cstdlib>
/* Problem parameters */
double f(double x);
double integral_serial(double xmin, double xmax, double n);
void integral_mpi(double xmin, double xmax, double n, int pid, int np);
int main(int argc, char **argv)
{
const int numberRects = std::atoi(argv[1]);
const double lowerLimit = 2.0;
const double upperLimit = 5.0;
/* MPI Variables */
/* problem variables */
int pid, np;
/* MPI setup */
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &np);
MPI_Comm_rank(MPI_COMM_WORLD, &pid);
integral_mpi(lowerLimit, upperLimit, numberRects, pid, np);
/* finish */
MPI_Finalize();
return 0;
}
double integral_serial(double xmin, double xmax, double n)
{
double area = 0.0;
double width = (xmax - xmin)/n;
for (int i = 0; i < n; ++i) {
double at = xmin + i*width + width/2.0; // center in the middle
double heigth = f(at);
area = area + width*heigth;
}
return area;
}
void integral_mpi(double xmin, double xmax, double n, int pid, int np)
{
/* Adjust problem size for sub-process */
double range = (xmax - xmin) / np;
double lower = xmin + range*pid;
/* Calculate area for subproblem */
double area = integral_serial(lower, lower+range, n);
/* Collect info and print results */
MPI_Status status;
int tag = 0;
if (0 == pid) { /* Master */
double total = area;
for (int src = 1; src < np; ++src) {
MPI_Recv(&area, 1, MPI_DOUBLE, src, tag, MPI_COMM_WORLD, &status);
total += area;
}
fprintf(stderr, "The area from %g to %g is : %25.16e\n", xmin, xmax, total);
}
else { /* slaves only send */
int dest = 0;
MPI_Send(&area, 1, MPI_DOUBLE, dest, tag, MPI_COMM_WORLD);
}
}
double f(double x) {
return x*x;
}
Compile as usual,
mpic++ mpi_integral.cpp
and run it
$ mpirun -np 2 ./a.out
$ mpirun -np 10 ./a.out
Exercise: Play with the number of processes. Are you getting a better answer for increasing number of processes?
In this example we have kept constant the number of rectangles per range. That means that as the number of processess increases, the total number of rectangles increases too, since each process has the same original number of rectangles. Therefore, the more the processes, the better the precision. If you prefer speed over precision, you will have to fix the total number of rectangles, whose number per processor will decrease.
Exercise : Change the previous code to handle a constant number of rectangles. As you increase the number of processors, is the precision increasing? or the speed?
The important part here is the scaling of the problem to the actual number of processes. For example, for five processes, we need first to divide the total interval (from 2 to 5 in tis example) into the number of processes, and then take each one of this sub-intervals and process it on the given process (identified by processId). This is called a domain-decomposition approach.
At the end of the code, we verify if we are on a slave or on the master.
If we are the master, we receive all the partial integrations sent by
the slaves, and then we print the total. If we are a slave, we just send
our result back to the master (destination = 0). Using these functions
is simple but not always efficient since, for example, for 100
processes, we are calling MPI_Send and MPI_Recv 99 times.
MPI_Send
used to send information to one process to another. A call to MPI_Send
MUST be matched with a corresponding MPI_Recv . Information is typed
(the type is explicitly stated), and tagged. The first argument of
MPI_Send gives the starting address of the data to be transmitted. The
second is the number of items to be sent, and the third one is the data
type (MPI_DOUBLE). There are more datatypes like MPI_BYTE,
MPI_CHAR, MPI_UNSIGNED, MPI_INT, MPI_FLOAT, MPI_PACKED, etc.
The next argument is the destination, that is, the rank of the receiver.
The next one is a tag, which is used for buffer purposes. Finally, the
(default) communicator is used.
MPI_Recv
allows to receive information sent by MPI_Send. Its first three
arguments are as before. Then it comes the destination (rank of the
receiving process), the tag, the communicator, and a status flag.
Both MPI_Send and MPI_Recv are blocking calls. If a process is
receiving information which has not been sent yet, if waits until it
receives that info without doing anything else.
Before continue, please check the following mpi functions:
MPI_ISend , MPI_IrecvMPI_SendrecvMPI_Sendrecv_replace
Exercise: Discuss if any of the previous can be used for the integral. Or what pattern would you think could be useful? maybe a reduction?
16.4. More Point to point exercises#
Check also: http://www.archer.ac.uk/training/course-material/2017/09/mpi-york/exercises/MPP-exercises.pdf
16.4.1. Ping-Pong#
Ref: Gavin, EPCC
Write an MPI code for 2 processes
The first task sends a message to the second task
The message can be a single integer
The second task receives this message
The second task changes the message somehow
Add 99 to the original message, for instance
The second task sends the message back to the first task
The first task receives the message
The first task prints this new message to the screen
Maybe repeat M times
16.4.2. Bandwitdh local and network#
Compute the bandwidth when sending data locally (same computer) and to other computer in the network. Plot the time taken to send the data as a function of the buffer size. Is the bandwidth (Mbits/s) constant? is there any difference between local and multimachine data sending?
16.4.3. Large unit matrix#
Imagine a large unit matrix that is distributed among all the processes in horizontal layers. Each process stores only its corresponding matrix part, not the full matrix. Make each process fill its corresponding part and then print the full matrix in the right order in the master process by sending each process matrix section to the master. Also plot it in gnupot or matplotlib
16.4.4. Ring pattern#
Ref: Gavin, EPCC
Write an MPI code which sends a message around a ring
Each MPI task receives from the left and passes that message on to the right
Every MPI task sends a message: Its own rank ID
How many steps are required for the message to return ‘home’.
Update the code so that each MPI Tasks takes the incoming message (an integer), and adds it to a running total
What should the answer be on MPI Task 0 . Is the answer the same on all tasks? (Test with unblocking send and even/odd send receive)
16.5. Collective Communications#
Check: https://mpitutorial.com/tutorials/mpi-broadcast-and-collective-communication/
If you check some of the previous code, or the integral code, we are
sending the same info over and over to every other process. While the
master sends the data to process 1, the remaining processes are idle.
This is not efficient. Fortunately, MPI provides several functions to
improve this situation, where the overall communication is managed much
better. The first function is MPI_Bcast.
MPI_Bcast
provides a mechanism to distribute the same information
among a communicator group, in an efficient manner. It takes five arguments. The first three are the data to be transmitted, as usual. The fourth one is the rank of the process generating the broadcast, a.k.a the root of the broadcast. The final argument is the communicator identifier. See: https://www.open-mpi.org/doc/v4.1/man3/MPI_Bcast.3.php . The syntax is
int MPI_Bcast(void *buffer, int count, MPI_Datatype datatype,
int root, MPI_Comm comm)
where root is the one sending the data in buffer to all other
processes.
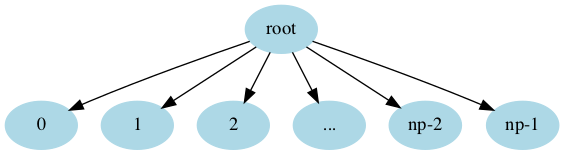
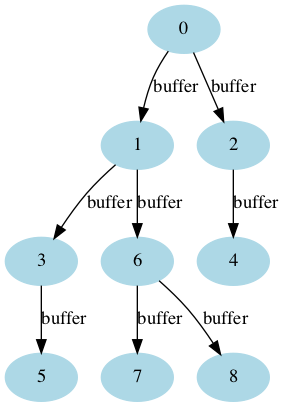
It could be internally optimized to reduce calls
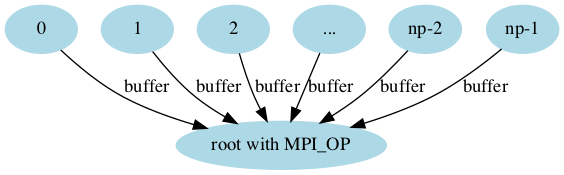
MPI_Reduce
allows to collect data and, at the same time, perform a
mathematical operation on it (like collecting the partial results and
then summing up them). It requires not only a place where to put the
results but also the operator to be applied. This could be, for example,
MPI_SUM, MPI_MIN, MPI_MAX, etc. It also needs the identifier of
the root of the broadcast. Both this functions will simplify a lot the
code, and also make it more efficient (since the data distribution and
gathering is optimised).
https://mpitutorial.com/tutorials/mpi-reduce-and-allreduce/
Check: https://mpitutorial.com/tutorials/mpi-broadcast-and-collective-communication/ http://wgropp.cs.illinois.edu/courses/cs598-s15/lectures/lecture29.pdf
16.5.1. MPI Bcast#
Sending an array from one source to all processes
#include "mpi.h" #include <iostream> #include <cstdlib> #include <algorithm> #include <numeric> void send_data_collective(int size, int pid, int np); int main(int argc, char **argv) { int np, pid; /* MPI setup */ MPI_Init(&argc, &argv); MPI_Comm_size(MPI_COMM_WORLD, &np); MPI_Comm_rank(MPI_COMM_WORLD, &pid); const int SIZE = std::atoi(argv[1]); send_data_collective(SIZE, pid, np); MPI_Finalize(); return 0; } void send_data_collective(int size, int pid, int np) { // create data buffer (all processes) double * data = new double [size]; if (0 == pid) { std::iota(data, data+size, 0.0); // llena como 0 1 2 3 4 } // send data to all processes int root = 0; double start = MPI_Wtime(); MPI_Bcast(&data[0], size, MPI_DOUBLE, root, MPI_COMM_WORLD); double end = MPI_Wtime(); // print size, time, bw in root if (0 == pid) { int datasize = sizeof(double)*size; std::cout << datasize << "\t" << (end-start) << "\t" << datasize/(end-start)/1.0e6 << "\n"; } delete [] data; }
[Minihomework] Mesuring the bandwidth and comparing with simple send and recv
#include "mpi.h" #include <iostream> #include <cstdlib> #include <algorithm> #include <numeric> void send_data_collective(int size, int pid, int np); void send_data_point_to_point(int size, int pid, int np); int main(int argc, char **argv) { int np, pid; /* MPI setup */ MPI_Init(&argc, &argv); MPI_Comm_size(MPI_COMM_WORLD, &np); MPI_Comm_rank(MPI_COMM_WORLD, &pid); const int SIZE = std::atoi(argv[1]); send_data_collective(SIZE, pid, np); MPI_Finalize(); return 0; } void send_data_point_to_point(int size, int pid, int np) { // ??? } void send_data_collective(int size, int pid, int np) { // create data buffer (all processes) double * data = new double [size]; std::iota(data, data+size, 0.0); // send data to all processes int root = 0; double start = MPI_Wtime(); MPI_Bcast(&data[0], size, MPI_DOUBLE, root, MPI_COMM_WORLD); double end = MPI_Wtime(); // print size, time, bw in root if (0 == pid) { int datasize = sizeof(double)*size; std::cout << datasize << "\t" << (end-start) << "\t" << datasize/(end-start)/1.0e6 << "\n"; } delete [] data; }
16.5.2. MPIBcast, MPIReduce#
In this case we will read some data in process 0 , then broadcast it to other processes, and finally reduce back some result (an integral , in this example).
#include "mpi.h"
#include <cstdio>
/* Problem parameters */
double f(double x);
int main(int argc, char **argv)
{
/* MPI Variables */
int dest, noProcesses, processId, src, tag;
MPI_Status status;
/* problem variables */
int i;
double area, at, heigth, width, total, range, lower;
int numberRects;
double lowerLimit;
double upperLimit;
/* MPI setup */
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &noProcesses);
MPI_Comm_rank(MPI_COMM_WORLD, &processId);
/* read, send, and receive parameters */
tag = 0;
if (0 == processId) {
fprintf(stderr, "Enter number of steps: \n");
scanf("%d", &numberRects);
fprintf(stderr, "Enter lower limit: \n");
scanf("%lf", &lowerLimit);
fprintf(stderr, "Enter upper limit: \n");
scanf("%lf", &upperLimit);
}
/* Broadcast the read data parameters*/
MPI_Bcast(&numberRects, 1, MPI_INT, 0, MPI_COMM_WORLD);
MPI_Bcast(&lowerLimit, 1, MPI_DOUBLE, 0, MPI_COMM_WORLD);
MPI_Bcast(&upperLimit, 1, MPI_DOUBLE, 0, MPI_COMM_WORLD);
/* Adjust problem size for sub-process */
range = (upperLimit - lowerLimit) / noProcesses;
width = range / numberRects;
lower = lowerLimit + range*processId;
/* Calculate area for subproblem */
area = 0.0;
for (i = 0; i < numberRects; ++i) {
at = lower + i*width + width/2.0;
heigth = f(at);
area = area + width*heigth;
}
/* Collect and reduce data */
MPI_Reduce(&area, &total, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
/* print results */
if (0 == processId) { /* Master */
std::fprintf(stderr, "The area from %g to %g is : %25.16e\n", lowerLimit, upperLimit, total);
}
/* finish */
MPI_Finalize();
return 0;
}
double f(double x) {
return x*x;
}
The eight functions MPI_Init, MPI_Comm_size, MPI_Comm_rank,
MPI_Send, MPI_Recv, MPI_Bcast, MPI_Reduce, and MPI_Finalize
are the core of the MPI programming. You are now and MPI programmer.
16.5.2.1. Exercises#
Modularize the previous integral code with functions. Basically use the same code as with send/recv but adapt it to use bcast/reduce.
Do the same for the problem of computing the L2 norm (Euclidean norm) of a very large vector. Fill it with ones and test the answer. What kind of cpu time scaling do you get as function of the number of processes, with N = 100000?
Filling randomly a matrix with probability \(p\): Make process 0 send the value of \(p\) to all processes. Also, distribute the matrix (only one slice per process). Fill the matrix at each process with prob \(p\). To verify, compute, at each process, the total places filled and send it to process 0. Add up all of them and print (from process 0) both the total proportion of filled sites (must be close to \(p\)) and the full matrix. Think if the algorithm that you devised to detect percolant clusters can be parallelized.
16.6. More examples : MPI_Gather, MPI_Scatter#
Check:
https://mpitutorial.com/tutorials/mpi-scatter-gather-and-allgather/
http://wgropp.cs.illinois.edu/courses/cs598-s15/lectures/lecture29.pdf
Functions :
MPI_Scatter:Sends parts of a given data to corresponding processes. Example: Array 16 doubles. You have 4 processes. Then this functions sends the first 4 doubles to rank 0, the second 4 doubles to rank 1, and so on. Note: The original array must exists on the sending process, so this might limit its size.MPI_Gather:It is the opposite. Recovers data from all processes and stores it on the root process.
Now let’s do some a program to practice them. This program will compute the average of a set of random numbers. We will try not to share the full array of random numbers, but instead to make each process create its own array. We will use a Gaussian random number generator with mean 1.23 and sigma 0.45:
Share with all processes the local array size (
N/np, whereNis the array size andnpis the number of processes), the mean and the sigma.Share with all process the seed for the local random number generator. The seed might be the rank. Store the seeds on a local array and then send them from rank 0.
Compute the local sum on each process.
Get the local sum by storing it on the seeds array (for now, don’t reduce).
Compute the mean and print it.
There are many other collective communications functions worth mentioning (https://en.wikipedia.org/wiki/Collective_operation , https://www.mpi-forum.org/docs/mpi-1.1/mpi-11-html/node64.html, https://www.rookiehpc.com/mpi/docs/index.php ):
MPIScatter and MPIGather
MPIAllGather and MPIAlltoall
MPIScatterv
MPIReduce, MPIScan, MPIExScan, ReduceScatter
Exercise: Each group will implement a working example of each of the following functions, as follows: https://www.rookiehpc.com/mpi/docs/index.php
Group |
Example |
|---|---|
1 |
MPIscatter and MPIGather, MPIallgather |
2 |
MPIScatterv, MPIGatherv |
3 |
MPIAlltoall, MPIalltoallv |
4 |
MPIReduce, MPIReducescatter |
5 |
MPIScan, MPIExscan |
6 |
MPIAll`Reduce with many MPIOP (min, max, sum , mult) |
16.6.1. Collective comms exercises#
Revisit all point-to-point comms exercises and implement them using collective comms if possible.
Ring code REF: Gavin, EPCC
Use a Collective Communications routine to produce the same result as your Ring Code so that only Task 0 ‘knows’ the answer.
Now change the Collective Communications call so all tasks ‘know’ the answer.
Can you think of another way to implement the collective communications routine than the Ring Code?
Compare the execution times for both the Ring Code and the associated Collective Communication routine.
Which is faster?
Why do the times change so much when you run it again and again?
What happens when the size of the message goes from 1 MPIINT to 10000 MPIINTs?!
Scaling for mpi integral Compute the scaling of the mpi integral code when using point to point and collective communications, in the same machine. Then do the same for two machines, dividing the number of processes among them.
You will compute the polynomial \(f(x) = x + x^{2} + x^{3} + x^{4} + \ldots + x^{N}\). Write an mpi program that computes this in \(N\) processes and prints the final value on master (id = 0) for \(x = 0.987654\) and \(N = 25\). Use broadcast communications when possible.
Compute the mean of a large array by distributing it on several processes. Your program must print the partial sums on each node and the final mean on master.
Compute the value of \(\pi\) by using the montecarlo method: Imagine a circle of radius 1. Its area would be \(\pi\). Imagine now the circle inscribed inside a square of length 2. Now compute the area (\(\pi\)) of the circle by using a simple Monte-Carlo procedure: just throw some random points inside the square (\(N_s\)) and count the number of points that fall inside the circle (\(N_c\)). The ratio of the areas is related with the ratio of inner points as \(A_c/A_s \simeq N_c/N_s\), therefore \(A_C \simeq A_s N_c/N_s\). Use as many processes as possible to increase the precision. At the end print the total number of points tested, the value of \(\pi\) found, and the percent difference with the expected value, \(\Delta\). Plot \(\Delta\) as function of \(N_p\).
16.7. Practical example: Parallel Relaxation method#
In this example we will parallelize the relaxation method by using MPI. We will decompose the domain, add some ghost zones and finally transmit some information between different processors. Our tasks will be as follows:
Probar la version serial.
Por cada proceso, crear el arreglo local incluyendo los ghosts: Probar llenando esta matriz con el pid y luego imprimir la matriz completa incluyendo y sin incluir los ghost (inicialización)
Paralelizar la inicializacion e imprimir comparando con la version serial.
Paralelizar las condiciones de frontera
Comunicacion entre procesos: Enviar y recibir de vecinos y guardar en las zonas ghost. Imprimir para verificar. Introducir y probar diversas formas de comunicación, como Send y Recv, llamadas no bloqueantes, Sendrecv, y MPINeighborªlltoallw con MPICreatecart.
Paralelizar la evolucion. Tener en cuenta las condiciones de frontera.
Medir metricas paralelas y medir el tiempo de comunicacion.
Extender a codiciones de frontera internas Usar un arreglo booleano que indique si una celda es frintera
Calcular tambien el campo y/o densidades de carga.
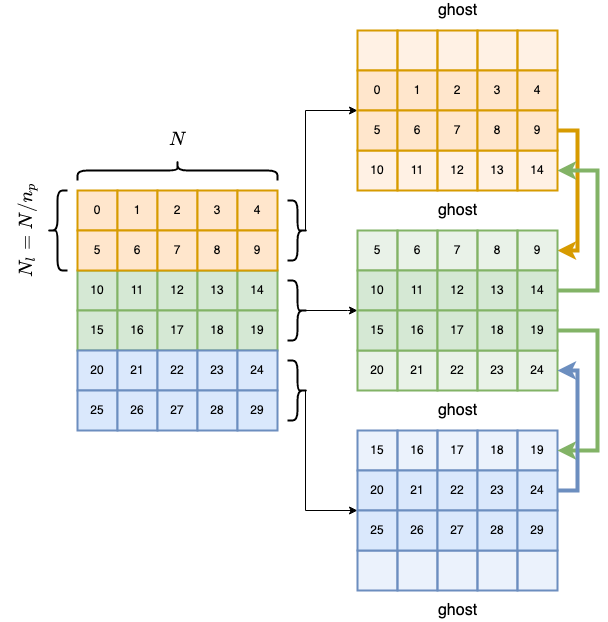
To decompose the domain, we will split the original matriz in horizontal
slices, one per processor (we assume \(N%n_p == 0\)). The data array, for
each processor, we will add two ghost rows to copy the boundary
information in order to make the evolution locally. Therefore, after
each update iteration, sync to the ghosts zones is needed. Locally each
array will be of size \((N_{l} +
2)\times N\), where \(N_l = N/n_p\) and there are 2 ghost rows. The
following diagram illustrates the process:
16.7.1. Serial version#
This version solves the Laplace equation by using the Jacbi-Gauss-Seidel relaxation method and prints gnuplot commands to create an animation.
#include <iostream>
#include <vector>
#include <cmath>
// constants
const double DELTA = 0.05;
const double L = 1.479;
const int N = int(L/DELTA)+1;
const int STEPS = 200;
typedef std::vector<double> Matrix; // alias
void initial_conditions(Matrix & m);
void boundary_conditions(Matrix & m);
void evolve(Matrix & m);
void print(const Matrix & m);
void init_gnuplot(void);
void plot_gnuplot(const Matrix & m);
int main(void)
{
Matrix data(N*N);
initial_conditions(data);
boundary_conditions(data);
//init_gnuplot();
for (int istep = 0; istep < STEPS; ++istep) {
evolve(data);
//plot_gnuplot(data);
if (istep == STEPS-1) {
print(data);
}
}
return 0;
}
void initial_conditions(Matrix & m)
{
for(int ii=0; ii<N; ++ii) {
for(int jj=0; jj<N; ++jj) {
m[ii*N + jj] = 1.0;
}
}
}
void boundary_conditions(Matrix & m)
{
int ii = 0, jj = 0;
ii = 0;
for (jj = 0; jj < N; ++jj)
m[ii*N + jj] = 100;
ii = N-1;
for (jj = 0; jj < N; ++jj)
m[ii*N + jj] = 0;
jj = 0;
for (ii = 1; ii < N-1; ++ii)
m[ii*N + jj] = 0;
jj = N-1;
for (ii = 1; ii < N-1; ++ii)
m[ii*N + jj] = 0;
}
void evolve(Matrix & m)
{
for(int ii=0; ii<N; ++ii) {
for(int jj=0; jj<N; ++jj) {
// check if boundary
if(ii == 0) continue;
if(ii == N-1) continue;
if(jj == 0) continue;
if(jj == N-1) continue;
// evolve non boundary
m[ii*N+jj] = (m[(ii+1)*N + jj] +
m[(ii-1)*N + jj] +
m[ii*N + jj + 1] +
m[ii*N + jj - 1] )/4.0;
}
}
}
void print(const Matrix & m)
{
for(int ii=0; ii<N; ++ii) {
for(int jj=0; jj<N; ++jj) {
std::cout << ii*DELTA << " " << jj*DELTA << " " << m[ii*N + jj] << "\n";
}
std::cout << "\n";
}
}
void init_gnuplot(void)
{
std::cout << "set contour " << std::endl;
std::cout << "set terminal gif animate " << std::endl;
std::cout << "set out 'anim.gif' " << std::endl;
}
void plot_gnuplot(const Matrix & m)
{
std::cout << "splot '-' w pm3d " << std::endl;
print(m);
std::cout << "e" << std::endl;
}
Exercise: Now just try to add the very basic mpi calls without actually parallelizing:
16.7.2. Parallelize both initial and boundary conditions#
The folowing code shows a possible parallelization for the initial conditions, plus some auxiliary functions to print the matrix using point to poin comms:
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include "mpi.h"
// constants
// const double DELTA = 0.05;
// const double L = 1.479;
// const int N = int(L/DELTA)+1;
// const int STEPS = 200;
typedef std::vector<double> Matrix; // alias
void initial_conditions(Matrix & m, int nrows, int ncols);
void boundary_conditions(Matrix & m, int nrows, int ncols);
void evolve(Matrix & m, int nrows, int ncols);
void print(const Matrix & m, double delta, int nrows, int ncols);
void init_gnuplot(void);
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols);
// parallel versions
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np);
void print_slab(const Matrix & m, int nrows, int ncols);
int main(int argc, char **argv)
{
MPI_Init(&argc, &argv);
int pid, np;
MPI_Comm_rank(MPI_COMM_WORLD, &pid);
MPI_Comm_size(MPI_COMM_WORLD, &np);
const int N = std::atoi(argv[1]);
const double L = std::atof(argv[2]);
const int STEPS = std::atoi(argv[3]);
const double DELTA = L/N;
// problem partition
int NCOLS = N, NROWS = N/np + 2; // include ghosts
Matrix data(NROWS*NCOLS); // include ghosts cells
initial_conditions(data, NROWS, NCOLS, pid, np);
if (0 == pid) {std::cout << " After initial conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np); // todo
boundary_conditions(data, NROWS, NCOLS, pid, np); // todo
if (0 == pid) {std::cout << " After boundary conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np); // todo
/*
// Serial version
Matrix data(N*N);
initial_conditions(data, N, N, ...);
print_screen(...);
boundary_conditions(data, N, N, ...);
init_gnuplot();
for (int istep = 0; istep < STEPS; ++istep) {
evolve(data, N, N);
plot_gnuplot(data, DELTA, N, N);
}
*/
MPI_Finalize();
return 0;
}
/////////////////////////////////////////////////////
// Parallel implementations
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// same task for all pids, but fill with the pids to distinguish among thems
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = pid;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// TODO
// Take into account each pid
}
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np)
{
// TODO
}
void print_slab(const Matrix & m, int nrows, int ncols)
{
// ignore ghosts
for(int ii = 1; ii < nrows-1; ++ii) {
for(int jj = 0; jj < ncols; ++jj) {
std::cout << std::setw(3) << m[ii*ncols + jj] << " ";
}
std::cout << "\n";
}
}
/////////////////////////////////////////////////////
// SERIAL VERSIONS
void initial_conditions(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = 1.0;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols)
{
int ii = 0, jj = 0;
ii = 0;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 100;
ii = nrows-1;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 0;
jj = 0;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
jj = ncols-1;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
}
void evolve(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
// check if boundary
if(ii == 0) continue;
if(ii == nrows-1) continue;
if(jj == 0) continue;
if(jj == ncols-1) continue;
// evolve non boundary
m[ii*ncols+jj] = (m[(ii+1)*ncols + jj] +
m[(ii-1)*ncols + jj] +
m[ii*ncols + jj + 1] +
m[ii*ncols + jj - 1] )/4.0;
}
}
}
void print(const Matrix & m, double delta, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
std::cout << ii*delta << " " << jj*delta << " " << m[ii*ncols + jj] << "\n";
}
std::cout << "\n";
}
}
void init_gnuplot(void)
{
std::cout << "set contour " << std::endl;
//std::cout << "set terminal gif animate " << std::endl;
//std::cout << "set out 'anim.gif' " << std::endl;
}
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols)
{
std::cout << "splot '-' w pm3d " << std::endl;
print(m, delta, nrows, ncols);
std::cout << "e" << std::endl;
}
Exercise
Complete the needed functions to paralelize the boundary conditions and printing.
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include "mpi.h"
typedef std::vector<double> Matrix; // alias
void initial_conditions(Matrix & m, int nrows, int ncols);
void boundary_conditions(Matrix & m, int nrows, int ncols);
void evolve(Matrix & m, int nrows, int ncols);
void print(const Matrix & m, double delta, int nrows, int ncols);
void init_gnuplot(void);
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols);
// parallel versions
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np);
void print_slab(const Matrix & m, int nrows, int ncols);
int main(int argc, char **argv)
{
MPI_Init(&argc, &argv);
int pid, np;
MPI_Comm_rank(MPI_COMM_WORLD, &pid);
MPI_Comm_size(MPI_COMM_WORLD, &np);
const int N = std::atoi(argv[1]);
const double L = std::atof(argv[2]);
const int STEPS = std::atoi(argv[3]);
const double DELTA = L/N;
// problem partition
int NCOLS = N, NROWS = N/np + 2; // include ghosts
Matrix data(NROWS*NCOLS); // include ghosts cells
initial_conditions(data, NROWS, NCOLS, pid, np);
if (0 == pid) {std::cout << " After initial conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np); // todo
boundary_conditions(data, NROWS, NCOLS, pid, np); // todo
if (0 == pid) {std::cout << " After boundary conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np); // todo
/*
// Serial version
Matrix data(N*N);
initial_conditions(data, N, N, ...);
print_screen(...);
boundary_conditions(data, N, N, ...);
init_gnuplot();
for (int istep = 0; istep < STEPS; ++istep) {
evolve(data, N, N);
plot_gnuplot(data, DELTA, N, N);
}
*/
MPI_Finalize();
return 0;
}
/////////////////////////////////////////////////////
// Parallel implementations
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// same task for all pids, but fill with the pids to distinguish among thems
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = pid;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// Take into account each pid
<<boundary-student>>
}
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np)
{
<<print-student>>
}
void print_slab(const Matrix & m, int nrows, int ncols)
{
// ignore ghosts
for(int ii = 1; ii < nrows-1; ++ii) {
for(int jj = 0; jj < ncols; ++jj) {
std::cout << std::setw(3) << m[ii*ncols + jj] << " ";
}
std::cout << "\n";
}
}
/////////////////////////////////////////////////////
// SERIAL VERSIONS
void initial_conditions(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = 1.0;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols)
{
int ii = 0, jj = 0;
ii = 0;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 100;
ii = nrows-1;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 0;
jj = 0;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
jj = ncols-1;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
}
void evolve(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
// check if boundary
if(ii == 0) continue;
if(ii == nrows-1) continue;
if(jj == 0) continue;
if(jj == ncols-1) continue;
// evolve non boundary
m[ii*ncols+jj] = (m[(ii+1)*ncols + jj] +
m[(ii-1)*ncols + jj] +
m[ii*ncols + jj + 1] +
m[ii*ncols + jj - 1] )/4.0;
}
}
}
void print(const Matrix & m, double delta, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
std::cout << ii*delta << " " << jj*delta << " " << m[ii*ncols + jj] << "\n";
}
std::cout << "\n";
}
}
void init_gnuplot(void)
{
std::cout << "set contour " << std::endl;
//std::cout << "set terminal gif animate " << std::endl;
//std::cout << "set out 'anim.gif' " << std::endl;
}
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols)
{
std::cout << "splot '-' w pm3d " << std::endl;
print(m, delta, nrows, ncols);
std::cout << "e" << std::endl;
}
You should get something like:
cd codes
mpic++ MPI_laplace_v1.cpp
mpirun -np 4 --oversubscribe ./a.out ./a.out 12 1.4705 1
After initial conditions ...
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2
3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3
After boundary conditions ...
0 100 100 100 100 100 100 100 100 100 100 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 0
0 2 2 2 2 2 2 2 2 2 2 0
0 2 2 2 2 2 2 2 2 2 2 0
0 2 2 2 2 2 2 2 2 2 2 0
0 3 3 3 3 3 3 3 3 3 3 0
0 3 3 3 3 3 3 3 3 3 3 0
0 0 0 0 0 0 0 0 0 0 0 0
16.7.3. Communication#
Here we explore how to implement the communication among the processes using the ring topology. Your task is to implement the communication in the following ways using
Typical Send and Recv calls
Using non-blocking sends
Using the function MPIsendrecv
Using MPIcreatecart and MPIneighbor alltoallw
Independet of the way it is implement, on step of comms must look like (ghost cells are printed and a new line added per process)
Exercise
Implement the communication pattern using simple senc and recv
TODO
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include "mpi.h"
typedef std::vector<double> Matrix; // alias
void initial_conditions(Matrix & m, int nrows, int ncols);
void boundary_conditions(Matrix & m, int nrows, int ncols);
void evolve(Matrix & m, int nrows, int ncols);
void print(const Matrix & m, double delta, int nrows, int ncols);
void init_gnuplot(void);
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols);
// parallel versions
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np, bool ghosts = false);
void print_slab(const Matrix & m, int nrows, int ncols, bool ghosts);
void send_rows(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_non_blocking(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_sendrecv(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_topology(Matrix & m, int nrows, int ncols, int pid, int np);
int main(int argc, char **argv)
{
MPI_Init(&argc, &argv);
int pid, np;
MPI_Comm_rank(MPI_COMM_WORLD, &pid);
MPI_Comm_size(MPI_COMM_WORLD, &np);
const int N = std::atoi(argv[1]);
const double L = std::atof(argv[2]);
const int STEPS = std::atoi(argv[3]);
const double DELTA = L/N;
// problem partition
int NCOLS = N, NROWS = N/np + 2; // include ghosts
Matrix data(NROWS*NCOLS); // include ghosts cells
initial_conditions(data, NROWS, NCOLS, pid, np);
if (0 == pid) {std::cout << " After initial conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np); // todo
boundary_conditions(data, NROWS, NCOLS, pid, np); // todo
if (0 == pid) {std::cout << " After boundary conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np, true); // todo
send_rows(data, NROWS, NCOLS, pid, np); // todo
//send_rows_non_blocking(data, NROWS, NCOLS, pid, np); // todo
//send_rows_sendrecv(data, NROWS, NCOLS, pid, np); // todo
//send_rows_topology(data, NROWS, NCOLS, pid, np); // todo
if (0 == pid) {std::cout << " After one comm ...\n";}
print_screen(data, NROWS, NCOLS, pid, np, true); // todo
/*
// Serial version
Matrix data(N*N);
initial_conditions(data, N, N, ...);
print_screen(...);
boundary_conditions(data, N, N, ...);
init_gnuplot();
for (int istep = 0; istep < STEPS; ++istep) {
evolve(data, N, N);
plot_gnuplot(data, DELTA, N, N);
}
*/
MPI_Finalize();
return 0;
}
/////////////////////////////////////////////////////
// Parallel implementations
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// same task for all pids, but fill with the pids to distinguish among thems
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = pid;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<boundary-student>>
}
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np, bool ghosts)
{
<<print-student>>
}
void print_slab(const Matrix & m, int nrows, int ncols, bool ghosts)
{
int imin = 0, imax = nrows;
if (false == ghosts) {
imin = 1; imax = nrows-1;
}
for(int ii = imin; ii < imax; ++ii) {
for(int jj = 0; jj < ncols; ++jj) {
std::cout << std::setw(3) << m[ii*ncols + jj] << " ";
}
std::cout << "\n";
}
std::cout << "\n";
}
void send_rows(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<send-rows-student>>
}
void send_rows_non_blocking(Matrix & m, int nrows, int ncols, int pid, int np)
{
// send data forwards
MPI_Request r1;
if (pid <= np-2) {
//MPI_Send(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD);
MPI_Isend(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, &r1);
}
if (pid >= 1) {
MPI_Recv(&m[0], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
// send data backwards
MPI_Request r2;
if (pid >= 1) {
MPI_Isend(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 1, MPI_COMM_WORLD, &r2);
}
if (pid <= np-2) {
MPI_Recv(&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 1, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (pid <= np-2) {
MPI_Wait(&r1, MPI_STATUS_IGNORE);
}
if (pid >= 1) {
MPI_Wait(&r2, MPI_STATUS_IGNORE);
}
}
void send_rows_sendrecv(Matrix & m, int nrows, int ncols, int pid, int np)
{
if (0 == pid) {
MPI_Sendrecv(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0,
&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (1 <= pid && pid <= np-2) {
// send data forwards
MPI_Sendrecv(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0,
&m[(0)*ncols], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// send data backwards
MPI_Sendrecv(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 0,
&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE); }
if (np-1 == pid) {
MPI_Sendrecv(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 0,
&m[(0)*ncols], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
}
void send_rows_topology(Matrix & m, int nrows, int ncols, int pid, int np)
{
// create a cartesian 1D topology representing the non-periodic ring
// https://wgropp.cs.illinois.edu/courses/cs598-s15/lectures/lecture28.pdf
// https://www.codingame.com/playgrounds/47058/have-fun-with-mpi-in-c/mpi-process-topologies
// MPI_Cart_create(MPI_Comm old_comm, int ndims, const int *dims, const int *periods, int reorder, MPI_Comm *comm_cart)
int ndims = 1, reorder = 1;
int dimsize[ndims] {np};
int periods[ndims] {0};
MPI_Comm comm;
MPI_Cart_create(MPI_COMM_WORLD, 1, &dimsize[0], &periods[0], reorder, &comm);
// Now use the network topology to communicate data in one pass for each direction
// https://www.open-mpi.org/doc/v3.0/man3/MPI_Neighbor_alltoallw.3.php
// https://www.events.prace-ri.eu/event/967/contributions/1110/attachments/1287/2213/MPI_virtual_topologies.pdf
MPI_Datatype types[2] = {MPI_DOUBLE, MPI_DOUBLE};
// NOTE: scounts[0] goes with rcounts[1] (left and right)
int scounts[2] = {ncols, ncols};
int rcounts[2] = {ncols, ncols};
MPI_Aint sdispl[2]{0}, rdispl[2] {0};
MPI_Get_address(&m[0]+(nrows-2)*ncols, &sdispl[1]); // send to next
MPI_Get_address(&m[0]+(0)*ncols, &rdispl[0]); // receive from previous
MPI_Get_address(&m[0]+(1)*ncols, &sdispl[0]); // send to previous
MPI_Get_address(&m[0]+(nrows-1)*ncols, &rdispl[1]); // receive from next
MPI_Neighbor_alltoallw(MPI_BOTTOM, scounts, sdispl, types,
MPI_BOTTOM, rcounts, rdispl, types, comm);
}
/////////////////////////////////////////////////////
// SERIAL VERSIONS
void initial_conditions(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = 1.0;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols)
{
int ii = 0, jj = 0;
ii = 0;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 100;
ii = nrows-1;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 0;
jj = 0;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
jj = ncols-1;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
}
void evolve(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
// check if boundary
if(ii == 0) continue;
if(ii == nrows-1) continue;
if(jj == 0) continue;
if(jj == ncols-1) continue;
// evolve non boundary
m[ii*ncols+jj] = (m[(ii+1)*ncols + jj] +
m[(ii-1)*ncols + jj] +
m[ii*ncols + jj + 1] +
m[ii*ncols + jj - 1] )/4.0;
}
}
}
void print(const Matrix & m, double delta, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
std::cout << ii*delta << " " << jj*delta << " " << m[ii*ncols + jj] << "\n";
}
std::cout << "\n";
}
}
void init_gnuplot(void)
{
std::cout << "set contour " << std::endl;
//std::cout << "set terminal gif animate " << std::endl;
//std::cout << "set out 'anim.gif' " << std::endl;
}
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols)
{
std::cout << "splot '-' w pm3d " << std::endl;
print(m, delta, nrows, ncols);
std::cout << "e" << std::endl;
}
// send data forwards
if (pid <= np-2) {
MPI_Send(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD);
}
if (pid >= 1) {
MPI_Recv(&m[0], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
// send data backwards
if (pid >= 1) {
MPI_Send(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 1, MPI_COMM_WORLD);
}
if (pid <= np-2) {
MPI_Recv(&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 1, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
❯ mpirun -np 6 --oversubscribe ./a.out 12 1.4705 1
After initial conditions ...
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2
3 3 3 3 3 3 3 3 3 3 3 3
3 3 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4 4 4 4 4 4 4
4 4 4 4 4 4 4 4 4 4 4 4
5 5 5 5 5 5 5 5 5 5 5 5
5 5 5 5 5 5 5 5 5 5 5 5
After boundary conditions ...
0 100 100 100 100 100 100 100 100 100 100 0
0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 0
0 2 2 2 2 2 2 2 2 2 2 0
0 2 2 2 2 2 2 2 2 2 2 0
0 3 3 3 3 3 3 3 3 3 3 0
0 3 3 3 3 3 3 3 3 3 3 0
0 4 4 4 4 4 4 4 4 4 4 0
0 4 4 4 4 4 4 4 4 4 4 0
0 5 5 5 5 5 5 5 5 5 5 0
0 0 0 0 0 0 0 0 0 0 0 0
After one comm ...
100 100 100 100 100 100 100 100 100 100 100 100
0 100 100 100 100 100 100 100 100 100 100 0
0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 1 1 0
0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 1 1 1 1 1 1 1 0
0 1 1 1 1 1 1 1 1 1 1 0
0 2 2 2 2 2 2 2 2 2 2 0
0 1 1 1 1 1 1 1 1 1 1 0
0 2 2 2 2 2 2 2 2 2 2 0
0 2 2 2 2 2 2 2 2 2 2 0
0 3 3 3 3 3 3 3 3 3 3 0
0 2 2 2 2 2 2 2 2 2 2 0
0 3 3 3 3 3 3 3 3 3 3 0
0 3 3 3 3 3 3 3 3 3 3 0
0 4 4 4 4 4 4 4 4 4 4 0
0 3 3 3 3 3 3 3 3 3 3 0
0 4 4 4 4 4 4 4 4 4 4 0
0 4 4 4 4 4 4 4 4 4 4 0
0 5 5 5 5 5 5 5 5 5 5 0
0 4 4 4 4 4 4 4 4 4 4 0
0 5 5 5 5 5 5 5 5 5 5 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
Exercise For a very large array, compute the bandwidth of each procedure as a function of the number of process.
16.7.4. Evolution#
In this case we will just move form the serial simple evolution to comms+evolution at each time step
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include "mpi.h"
typedef std::vector<double> Matrix; // alias
void initial_conditions(Matrix & m, int nrows, int ncols);
void boundary_conditions(Matrix & m, int nrows, int ncols);
void evolve(Matrix & m, int nrows, int ncols);
void print(const Matrix & m, double delta, int nrows, int ncols);
void init_gnuplot(void);
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols);
// parallel versions
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np, bool ghosts = false);
void print_slab(const Matrix & m, int nrows, int ncols, bool ghosts);
void send_rows(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_non_blocking(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_sendrecv(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_topology(Matrix & m, int nrows, int ncols, int pid, int np);
void evolve(Matrix & m, int nrows, int ncols, int pid, int np);
int main(int argc, char **argv)
{
MPI_Init(&argc, &argv);
int pid, np;
MPI_Comm_rank(MPI_COMM_WORLD, &pid);
MPI_Comm_size(MPI_COMM_WORLD, &np);
const int N = std::atoi(argv[1]);
const double L = std::atof(argv[2]);
const int STEPS = std::atoi(argv[3]);
const double DELTA = L/N;
// problem partition
int NCOLS = N, NROWS = N/np + 2; // include ghosts
Matrix data(NROWS*NCOLS); // include ghosts cells
initial_conditions(data, NROWS, NCOLS, pid, np);
if (0 == pid) {std::cout << " After initial conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np); // todo
boundary_conditions(data, NROWS, NCOLS, pid, np); // todo
if (0 == pid) {std::cout << " After boundary conditions ...\n";}
print_screen(data, NROWS, NCOLS, pid, np, true); // todo
//send_rows(data, NROWS, NCOLS, pid, np); // todo
//send_rows_non_blocking(data, NROWS, NCOLS, pid, np); // todo
//send_rows_sendrecv(data, NROWS, NCOLS, pid, np); // todo
send_rows_topology(data, NROWS, NCOLS, pid, np); // todo
if (0 == pid) {std::cout << " After one comm ...\n";}
print_screen(data, NROWS, NCOLS, pid, np, true); // todo
if (0 == pid) {std::cout << " After one relax step ...\n";}
evolve(data, NROWS, NCOLS, pid, np);
send_rows_topology(data, NROWS, NCOLS, pid, np); // todo
print_screen(data, NROWS, NCOLS, pid, np, true); // todo
if (0 == pid) {std::cout << " After one relax step ...\n";}
evolve(data, NROWS, NCOLS, pid, np);
send_rows_topology(data, NROWS, NCOLS, pid, np); // todo
print_screen(data, NROWS, NCOLS, pid, np, true); // todo
/*
// Serial version
Matrix data(N*N);
initial_conditions(data, N, N, ...);
print_screen(...);
boundary_conditions(data, N, N, ...);
init_gnuplot();
for (int istep = 0; istep < STEPS; ++istep) {
evolve(data, N, N);
plot_gnuplot(data, DELTA, N, N);
}
*/
MPI_Finalize();
return 0;
}
/////////////////////////////////////////////////////
// Parallel implementations
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// same task for all pids, but fill with the pids to distinguish among thems
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = pid;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<boundary-student>>
}
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np, bool ghosts)
{
<<print-student>>
}
void print_slab(const Matrix & m, int nrows, int ncols, bool ghosts)
{
int imin = 0, imax = nrows;
if (false == ghosts) {
imin = 1; imax = nrows-1;
}
std::cout.precision(3);
for(int ii = imin; ii < imax; ++ii) {
for(int jj = 0; jj < ncols; ++jj) {
std::cout << std::setw(9) << m[ii*ncols + jj] << " ";
}
std::cout << "\n";
}
std::cout << "\n";
}
void send_rows(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<send-rows-student>>
}
void send_rows_non_blocking(Matrix & m, int nrows, int ncols, int pid, int np)
{
// send data forwards
MPI_Request r1;
if (pid <= np-2) {
//MPI_Send(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD);
MPI_Isend(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, &r1);
}
if (pid >= 1) {
MPI_Recv(&m[0], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
// send data backwards
MPI_Request r2;
if (pid >= 1) {
MPI_Isend(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 1, MPI_COMM_WORLD, &r2);
}
if (pid <= np-2) {
MPI_Recv(&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 1, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (pid <= np-2) {
MPI_Wait(&r1, MPI_STATUS_IGNORE);
}
if (pid >= 1) {
MPI_Wait(&r2, MPI_STATUS_IGNORE);
}
}
void send_rows_sendrecv(Matrix & m, int nrows, int ncols, int pid, int np)
{
if (0 == pid) {
MPI_Sendrecv(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0,
&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (1 <= pid && pid <= np-2) {
// send data forwards
MPI_Sendrecv(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0,
&m[(0)*ncols], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// send data backwards
MPI_Sendrecv(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 0,
&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE); }
if (np-1 == pid) {
MPI_Sendrecv(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 0,
&m[(0)*ncols], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
}
void send_rows_topology(Matrix & m, int nrows, int ncols, int pid, int np)
{
// create a cartesian 1D topology representing the non-periodic ring
// https://wgropp.cs.illinois.edu/courses/cs598-s15/lectures/lecture28.pdf
// https://www.codingame.com/playgrounds/47058/have-fun-with-mpi-in-c/mpi-process-topologies
// MPI_Cart_create(MPI_Comm old_comm, int ndims, const int *dims, const int *periods, int reorder, MPI_Comm *comm_cart)
int ndims = 1, reorder = 1;
int dimsize[ndims] {np};
int periods[ndims] {0};
MPI_Comm comm;
MPI_Cart_create(MPI_COMM_WORLD, 1, &dimsize[0], &periods[0], reorder, &comm);
// Now use the network topology to communicate data in one pass for each direction
// https://www.open-mpi.org/doc/v3.0/man3/MPI_Neighbor_alltoallw.3.php
// https://www.events.prace-ri.eu/event/967/contributions/1110/attachments/1287/2213/MPI_virtual_topologies.pdf
MPI_Datatype types[2] = {MPI_DOUBLE, MPI_DOUBLE};
// NOTE: scounts[0] goes with rcounts[1] (left and right)
int scounts[2] = {ncols, ncols};
int rcounts[2] = {ncols, ncols};
MPI_Aint sdispl[2]{0}, rdispl[2] {0};
MPI_Get_address(&m[0]+(nrows-2)*ncols, &sdispl[1]); // send to next
MPI_Get_address(&m[0]+(0)*ncols, &rdispl[0]); // receive from previous
MPI_Get_address(&m[0]+(1)*ncols, &sdispl[0]); // send to previous
MPI_Get_address(&m[0]+(nrows-1)*ncols, &rdispl[1]); // receive from next
MPI_Neighbor_alltoallw(MPI_BOTTOM, scounts, sdispl, types,
MPI_BOTTOM, rcounts, rdispl, types, comm);
}
void evolve(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<evolve-student>>
}
/////////////////////////////////////////////////////
// SERIAL VERSIONS
void initial_conditions(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = 1.0;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols)
{
int ii = 0, jj = 0;
ii = 0;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 100;
ii = nrows-1;
for (jj = 0; jj < ncols; ++jj)
m[ii*ncols + jj] = 0;
jj = 0;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
jj = ncols-1;
for (ii = 1; ii < nrows-1; ++ii)
m[ii*ncols + jj] = 0;
}
void evolve(Matrix & m, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
// check if boundary
if(ii == 0) continue;
if(ii == nrows-1) continue;
if(jj == 0) continue;
if(jj == ncols-1) continue;
// evolve non boundary
m[ii*ncols+jj] = (m[(ii+1)*ncols + jj] +
m[(ii-1)*ncols + jj] +
m[ii*ncols + jj + 1] +
m[ii*ncols + jj - 1] )/4.0;
}
}
}
void print(const Matrix & m, double delta, int nrows, int ncols)
{
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
std::cout << ii*delta << " " << jj*delta << " " << m[ii*ncols + jj] << "\n";
}
std::cout << "\n";
}
}
void init_gnuplot(void)
{
std::cout << "set contour " << std::endl;
//std::cout << "set terminal gif animate " << std::endl;
//std::cout << "set out 'anim.gif' " << std::endl;
}
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols)
{
std::cout << "splot '-' w pm3d " << std::endl;
print(m, delta, nrows, ncols);
std::cout << "e" << std::endl;
}
Now we can just perform the relaxation step many times and create the animation after parallelizing gnuplot printing:
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
#include "mpi.h"
typedef std::vector<double> Matrix; // alias
void initial_conditions(Matrix & m, int nrows, int ncols);
void boundary_conditions(Matrix & m, int nrows, int ncols);
void evolve(Matrix & m, int nrows, int ncols);
void print(const Matrix & m, double delta, int nrows, int ncols);
void init_gnuplot(void);
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols);
// parallel versions
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np);
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np, bool ghosts = false);
void print_slab(const Matrix & m, int nrows, int ncols, bool ghosts);
void send_rows(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_non_blocking(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_sendrecv(Matrix & m, int nrows, int ncols, int pid, int np);
void send_rows_topology(Matrix & m, int nrows, int ncols, int pid, int np);
void evolve(Matrix & m, int nrows, int ncols, int pid, int np);
void init_gnuplot(int pid, int np);
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols, int pid, int np);
void print_slab_gnuplot(const Matrix & m, double delta, int nrows, int ncols, int pid, int np);
int main(int argc, char **argv)
{
MPI_Init(&argc, &argv);
int pid, np;
MPI_Comm_rank(MPI_COMM_WORLD, &pid);
MPI_Comm_size(MPI_COMM_WORLD, &np);
const int N = std::atoi(argv[1]);
const double L = std::atof(argv[2]);
const int STEPS = std::atoi(argv[3]);
const double DELTA = L/N;
// problem partition
int NCOLS = N, NROWS = N/np + 2; // include ghosts
Matrix data(NROWS*NCOLS); // include ghosts cells
initial_conditions(data, NROWS, NCOLS, pid, np);
//if (0 == pid) {std::cout << " After initial conditions ...\n";}
//print_screen(data, NROWS, NCOLS, pid, np); // todo
boundary_conditions(data, NROWS, NCOLS, pid, np); // todo
//if (0 == pid) {std::cout << " After boundary conditions ...\n";}
//print_screen(data, NROWS, NCOLS, pid, np, true); // todo
<<anim-student>>
MPI_Finalize();
return 0;
}
/////////////////////////////////////////////////////
// Parallel implementations
void initial_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
// same task for all pids, but fill with the pids to distinguish among thems
for(int ii=0; ii<nrows; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
m[ii*ncols + jj] = pid;
}
}
}
void boundary_conditions(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<boundary-student>>
}
void print_screen(const Matrix & m, int nrows, int ncols, int pid, int np, bool ghosts)
{
<<print-student>>
}
void print_slab(const Matrix & m, int nrows, int ncols, bool ghosts)
{
int imin = 0, imax = nrows;
if (false == ghosts) {
imin = 1; imax = nrows-1;
}
std::cout.precision(3);
for(int ii = imin; ii < imax; ++ii) {
for(int jj = 0; jj < ncols; ++jj) {
std::cout << std::setw(9) << m[ii*ncols + jj] << " ";
}
std::cout << "\n";
}
std::cout << "\n";
}
void send_rows(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<send-rows-student>>
}
void send_rows_non_blocking(Matrix & m, int nrows, int ncols, int pid, int np)
{
// send data forwards
MPI_Request r1;
if (pid <= np-2) {
//MPI_Send(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD);
MPI_Isend(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, &r1);
}
if (pid >= 1) {
MPI_Recv(&m[0], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
// send data backwards
MPI_Request r2;
if (pid >= 1) {
MPI_Isend(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 1, MPI_COMM_WORLD, &r2);
}
if (pid <= np-2) {
MPI_Recv(&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 1, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (pid <= np-2) {
MPI_Wait(&r1, MPI_STATUS_IGNORE);
}
if (pid >= 1) {
MPI_Wait(&r2, MPI_STATUS_IGNORE);
}
}
void send_rows_sendrecv(Matrix & m, int nrows, int ncols, int pid, int np)
{
if (0 == pid) {
MPI_Sendrecv(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0,
&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
if (1 <= pid && pid <= np-2) {
// send data forwards
MPI_Sendrecv(&m[(nrows-2)*ncols], ncols, MPI_DOUBLE, pid+1, 0,
&m[(0)*ncols], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
// send data backwards
MPI_Sendrecv(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 0,
&m[(nrows-1)*ncols], ncols, MPI_DOUBLE, pid+1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE); }
if (np-1 == pid) {
MPI_Sendrecv(&m[(1)*ncols], ncols, MPI_DOUBLE, pid-1, 0,
&m[(0)*ncols], ncols, MPI_DOUBLE, pid-1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
}
void send_rows_topology(Matrix & m, int nrows, int ncols, int pid, int np)
{
// create a cartesian 1D topology representing the non-periodic ring
// https://wgropp.cs.illinois.edu/courses/cs598-s15/lectures/lecture28.pdf
// https://www.codingame.com/playgrounds/47058/have-fun-with-mpi-in-c/mpi-process-topologies
// MPI_Cart_create(MPI_Comm old_comm, int ndims, const int *dims, const int *periods, int reorder, MPI_Comm *comm_cart)
int ndims = 1, reorder = 1;
int dimsize[ndims] {np};
int periods[ndims] {0};
MPI_Comm comm;
MPI_Cart_create(MPI_COMM_WORLD, 1, &dimsize[0], &periods[0], reorder, &comm);
// Now use the network topology to communicate data in one pass for each direction
// https://www.open-mpi.org/doc/v3.0/man3/MPI_Neighbor_alltoallw.3.php
// https://www.events.prace-ri.eu/event/967/contributions/1110/attachments/1287/2213/MPI_virtual_topologies.pdf
MPI_Datatype types[2] = {MPI_DOUBLE, MPI_DOUBLE};
// NOTE: scounts[0] goes with rcounts[1] (left and right)
int scounts[2] = {ncols, ncols};
int rcounts[2] = {ncols, ncols};
MPI_Aint sdispl[2]{0}, rdispl[2] {0};
MPI_Get_address(&m[0]+(nrows-2)*ncols, &sdispl[1]); // send to next
MPI_Get_address(&m[0]+(0)*ncols, &rdispl[0]); // receive from previous
MPI_Get_address(&m[0]+(1)*ncols, &sdispl[0]); // send to previous
MPI_Get_address(&m[0]+(nrows-1)*ncols, &rdispl[1]); // receive from next
MPI_Neighbor_alltoallw(MPI_BOTTOM, scounts, sdispl, types,
MPI_BOTTOM, rcounts, rdispl, types, comm);
}
void evolve(Matrix & m, int nrows, int ncols, int pid, int np)
{
<<evolve-student>>
}
void init_gnuplot(int pid, int np)
{
if (0 == pid) {
std::cout << "set contour " << std::endl;
std::cout << "set terminal gif animate " << std::endl;
std::cout << "set out 'anim.gif' " << std::endl;
}
}
void plot_gnuplot(const Matrix & m, double delta, int nrows, int ncols, int pid, int np)
{
if (0 == pid) {
std::cout << "splot '-' w pm3d " << std::endl;
// print master data
print_slab_gnuplot(m, delta, nrows, ncols, pid, np);
// now receive and print other pdis data
Matrix buffer(nrows*ncols);
for (int ipid = 1; ipid < np; ++ipid) {
MPI_Recv(&buffer[0], nrows*ncols, MPI_DOUBLE, ipid, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
print_slab_gnuplot(buffer, delta, nrows, ncols, pid, np);
}
std::cout << "e" << std::endl;
} else { // workers send
MPI_Send(&m[0], nrows*ncols, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
}
}
void print_slab_gnuplot(const Matrix & m, double delta, int nrows, int ncols, int pid, int np)
{
// needs to fix local index with global ones
// ignore ghosts
for(int ii=1; ii<nrows-1; ++ii) {
for(int jj=0; jj<ncols; ++jj) {
std::cout << (ii-1 + nrows*pid)*delta << " " << (jj-1)*delta << " " << m[ii*ncols + jj] << "\n";
}
std::cout << "\n";
}
}
16.7.5. Example: Running the laplace mpi simulation using slurm#
Here we will use at least two nodes to run the laplace simulation. Of course the performance will be affected since our network is slow, but the goal here is to be able to run the command.
#!/usr/bin/env bash
#SBATCH --job-name="testmulti"
# #SBATCH --account="HerrComp" # not used
#SBATCH --mail-type=ALL
#SBATCH --mail-user=wfoquendop@unal.edu.co
#SBATCH --time=01:00:00
#SBATCH --nodes=3
#SBATCH --ntasks-per-node=6
#SBATCH --cpus-per-task=1
#SBATCH --partition=12threads
export OMP_NUM_THREADS=$SLURM_CPUS_PER_TASK
cd $HOME/repos/2021-II-HerrComp/2022-02-09-Slurm/
mpic++ MPI_laplace_v5.cpp
date
srun --mpi=pmi2 ./a.out 180 1.4705 200 | gnuplot
date
16.7.5.1. Exercises#
Parallelize the code used on the relaxation method to solve the Poisson equation, including some charge densities and some ineer boundary conditions. Here you will need to decompose the domain, keep some ghost zones, and share some info across processes to update the ghost zones.
16.8. Debugging in parallel#
https://stackoverflow.com/questions/329259/how-do-i-debug-an-mpi-program
https://hpc.llnl.gov/software/development-environment-software/stat-stack-trace-analysis-tool
wget https://epcced.github.io/2022-04-19-archer2-intro-develop/files/gdb4hpc_exercise.c


