Errors in numerical computation: Floating point numbers

3. Errors in numerical computation: Floating point numbers#

Image Description
From: "https://upload.wikimedia.org/wikipedia/commons/thumb/b/b6/FloatingPointPrecisionAugmented.png/1000px-FloatingPointPrecisionAugmented.png"

  • To avoid differences across platforms, the IEE754 standard stablished rules for approximation, truncation, and so on. https://en.wikipedia.org/wiki/IEEE_754?useskin=vector . Languages like c/c++/fortran/python support the standard. In particular, for scientific applications try to use ‘double’ precission

  • There are several possible representation of floating point numbers, like Fixed point (https://en.wikipedia.org/wiki/Fixed-point_arithmetic), decimal representation, etc, but the common one in the IEEE754 standard is an “exponential” scientific notation. Play with https://bartaz.github.io/ieee754-visualization/

    Format

    bits

    exponent bits

    Significand bits

    Machine eps

    float

    32

    8

    23

    \(10^{-7}\)

    double

    64

    11

    52

    \(10^{-16}\)
under-over-truncation

Some warnings:

  • 14 decimal places can be lost in a single operation.

  • Do not cast floats to integers and viceversa

  • Addition is no longer associative: \(x + (y+z) != (x+y) + z \). Use \(x = +1.5e38, y = -1.5e38, z = 1\).

  • Not every number can be exactly represented (1/3, 0.1, etc)

  • Compilers has many flags, explore them (-ffast-math, -ffloat-store).

  • Beware of fast math: https://simonbyrne.github.io/notes/fastmath/

For some dramatic examples of FP errors, check:

3.1. Overflow for integers#

Overflow occurs when you try to represent a number larger than the allowed for that datatype. Please find the integer types limits, and now look for the actual occurrence by implementing the following algorithm:

  • start with a var = 1

  • then multiply by 2 and print the number. Do this for both int and long datatypes. Are the maximum representative values as expected? are the same for both datatypes?

#include <cstdio>

int main(void)
{
    int a = 1;

    // TODO

    return 0;
}

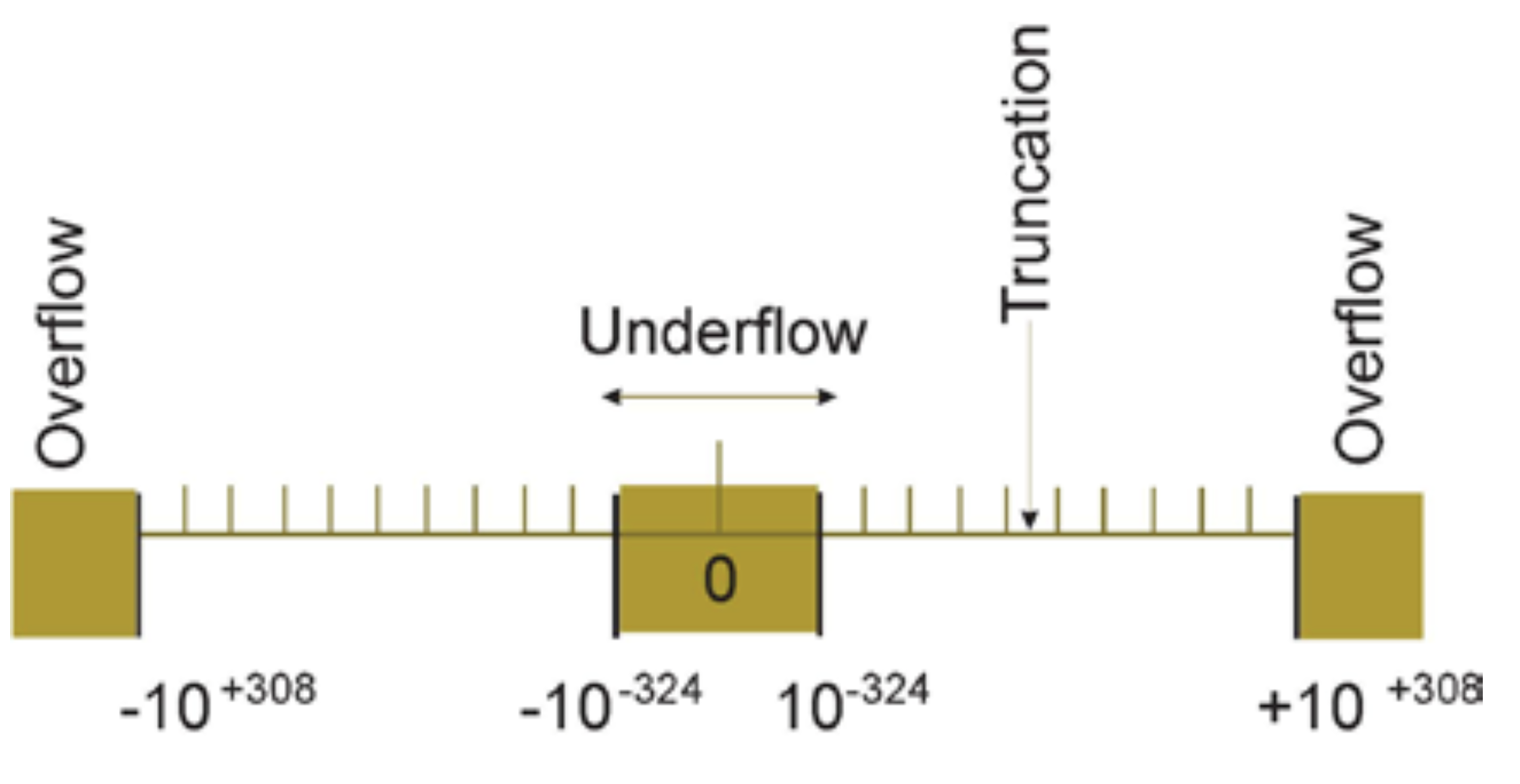
3.2. Underflow and overflow for floats#

Underflow means representing a value smaller than the one allowed. What happens when you reach an overflow? let’s find it.

Notice that this code reads an argument from the command line (which is the total number of steps to perform. For the overflow, multiply by 2, for underflow, divide by 2.

#include <iostream>
#include <cstdlib>

typedef float REAL;

int main(int argc, char **argv)
{
    std::cout.precision(16);
    std::cout.setf(std::ios::scientific);
    int N = std::atoi(argv[1]);
    REAL under = 1.0, over = 1.0;

    //TODO

    return 0;
}

3.3. Machine eps#

You can also compute/verify the machine precision \(\epsilon_m\) of your machine according to different types. The machine precision is a number that basically rounds to zero and in opertation. It can be represented as \(1_c + \epsilon_m = 1_c\), where \(1_c\) is the computational representation of the number 1. Actually, that means than any real number \(x\) is actually represented as $\(x_c = x(1+\epsilon), |\epsilon| \le \epsilon_m .\)$

Implement the following algorithm to compute it and report your results:

eps = 1.0
begin do N times
    eps = eps/2.0
    one = 1.0 + eps
    print

#include <iostream>
#include <cstdlib>

typedef float REAL;

int main(int argc, char **argv)
{   
  std::cout.precision(20);
  std::cout.setf(std::ios::scientific);

    // TODO
    
  return 0;
}

3.4. Practical example: Series expansion of \(e^{-x}\)#

The function \(e^{-x}\) can be expanded as

(3.1)#\[\begin{equation} e^{-x} = \sum_{i=0}^{\infty} (-1)^i \frac{x^i}{i!} = 1 - x + \frac{x^2}{2} - \frac{x^3}{6} + \ldots \ (|x| < \infty) \end{equation}\]

This is a great expansion, valid for all finite values of \(x\). But, what numerical problems do you see?

Implement a function that receives \(x\) and \(N\) (max number of terms), and saves the iteration value of the series as a function of \(i\) in a file called sumdata.txt. Then load the data and plot it. Use \(N = 10000\) and \(x=1.8766\). You will need to implement also a factorial function.

#include <iostream>
#include <cmath>

typedef float REAL;

int factorial(int n);
REAL fnaive(REAL x, int N);
REAL fsmart(REAL x, int N);

int main(void)
{
  std::cout.precision(16); std::cout.setf(std::ios::scientific);
  REAL x = 1.234534534;
  const REAL exact = std::exp(-x);
  for (int NMAX = 0; NMAX <= 100; ++NMAX) {
    std::cout << NMAX
              << "\t" << fnaive(x, NMAX)
              << "\t" << std::fabs(fnaive(x, NMAX) - exact)/exact
              << "\t" << fsmart(x, NMAX)
              << "\t" << std::fabs(fsmart(x, NMAX) - exact)/exact
              << std::endl;
  }
  return 0;
}

REAL fnaive(REAL x, int N)
{
    //TODO
    
}

int factorial(int n)
{
  if (n <= 0) return 1;
  return n*factorial(n-1);
}

REAL fsmart(REAL x, int N)
{
    //TODO
}

3.4.1. Exercise: Substractive cancellation with the Quadratic equation#

3.4.2. Exercise: Sum ups and down#

Is there any computation difference between the following sums?

(3.2)#\[\begin{align} S_{up}(N) &= \sum_{n=1}^{N} \frac{1}{n},\\ S_{down}(N) &= \sum_{n=N}^{1} \frac{1}{n}. \end{align}\]

Implement and plot the relative difference among them as a function of \(N\).

3.5. Errors#

  • FP is well defined through the IEEE754 standard.

  • A simple substraction could destroy 15 decimal places of precision

  • You should not cast floats to integers

  • You should normalize your models to natural units

  • Addition is not always associative: \(x + (y + z) \ne (x+y) + z\), when \(x = -1.5\times 10^{38}, y = +1.5\times 10^{38}, z = 1.0\) (single precision)

  • All numbers can be represented in binary: false. Check 0.1, or 0.3

For some dramatic examples of FP errors, check:

  • https://www.iro.umontreal.ca/~mignotte/IFT2425/Disasters.html

  • https://web.ma.utexas.edu/users/arbogast/misc/disasters.html

  • https://slate.com/technology/2019/10/round-floor-software-errors-stock-market-battlefield.html

  • https://stackoverflow.com/questions/2732845/real-life-example-fo-floating-point-error

Kind of errors

  • Probability of an error: start \(\to U_1 \to U_2 \to \ldots \to U_n \to\) end

  • Blunders: Typographical, wrong program, etc

  • Random errors: Electronics, alien invasion, etc

  • Approximation: (mathematical series truncation)

  • Roundoff and truncation of a number in the computer representation

3.5.1. Test for associativity#

Sometimes there is also no associativity. Explain the following code and its result.

#include <cstdio>

int main(void)
{
  float x = -1.5e38, y = 1.5e38, z = 1;
  printf("%16.6f\t%16.6f\n", x + (y+z), (x+y) + z);
  printf("%16.16f\n", 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1);

  return 0;
}

3.5.2. Roundoff/truncation example#

Let’s compute the following sum as a function of \(k\),

(3.3)#\[\begin{equation} f(k) = \left|\frac{k}{10} - \sum_{i=1}^k 0.1\right| \end{equation}\]

Mathematically, this function should give 0 always. Is that true?

3.5.3. Substractive cancellation#

Given \(a = b-c\), then \(a_c = b_c-c_c\), therefore

(3.4)#\[\begin{align} a_c &= a(1+\epsilon_a ) = b_c - c_c = b(1+\epsilon_b ) - c(1+\epsilon_c )\\ \frac{a_c}{a} &= 1 + \epsilon_b \frac{b}{a} - \frac{c}{a}\epsilon_c \end{align}\]

so the error in \(a\) is about

(3.5)#\[\begin{equation} \epsilon_a = \frac{b}{a}(\epsilon_b - \epsilon_c), \end{equation}\]

which is much larger, when \(b\) and \(c\) are close (so \(a\) is small).

3.5.3.1. Example of substrative cancellation#

The following series,

(3.6)#\[\begin{equation} S_N^{(1)} = \sum_{n=1}^{2N} (-1)^n \frac{n}{n+1}, \end{equation}\]

can be written in two mathematically equivalent ways:

(3.7)#\[\begin{equation} S_N^{(2)} = -\sum_{n=1}^{N} \frac{2n-1}{2n} + \sum_{n=1}^{N} \frac{2n}{2n+1}, \end{equation}\]

and

(3.8)#\[\begin{equation} S_N^{(3)} = \sum_{n=1}^{N} \frac{1}{2n(2n+1)}. \end{equation}\]

Could there be any computational difference? why?

Write a program that compute all sums, and , assuming that \(S_n^{(3)}\) is the best option (why?), plots the relative difference with the other sums as a function of \(N\).

3.6. Total errors in algorithms and their computational implementation#

As you can see, there are several source for errors in computation. Some come from the mathematical approximation, , called \(\epsilon_a\), and some others are intrinsic from the numerical representation, and we can call them \(\epsilon_r\). Sometimes, the rounding/truncation error are modeled as a random walk, \(\epsilon_r \simeq \sqrt{N} \epsilon_m\), where \(\epsilon_m\) is the machine precision, and \(N\) is the representative number of “steps”. From here, the total error can be estimated as

(3.9)#\[\begin{align} \epsilon_{\rm tot} &= \epsilon_a + \epsilon_r \\ &= \frac{\alpha}{N^\beta} + \sqrt{N} \epsilon_m. \end{align}\]

You can derive this equation an compute the optimal value for \(N\), which will depend on the order of the mathematical algorithm and the machine precision. The next table show some examples that illustrate this point:

under-over-truncation

3.7. How to minimize numerical errors?#

Contents