Standard library of functions: math functions, containers and random numbers

5. Standard library of functions: math functions, containers and random numbers#

The C++ Standard Template Library (STL) is a powerful collection of template classes and functions that provide general-purpose data structures and algorithms. Core components include containers (such as vectors, lists, maps, and sets), iterators for traversing these containers, algorithms for searching and sorting, function objects, and adaptors. The STL emphasizes generic programming through templates, allowing operations to work with different data types while maintaining type safety and performance. Its design principles of abstraction, efficiency, and reusability have made it an essential part of modern C++ programming, enabling developers to write cleaner, more maintainable code with less effort.

Check: https://en.cppreference.com/w/

5.1. Random numbers#

https://en.cppreference.com/w/cpp/numeric/random We need:

A random bit generator (mersenne-twsiter and so on)
A random distribution

From: "https://hackingcpp.com/cpp/std/random_distributions.png"

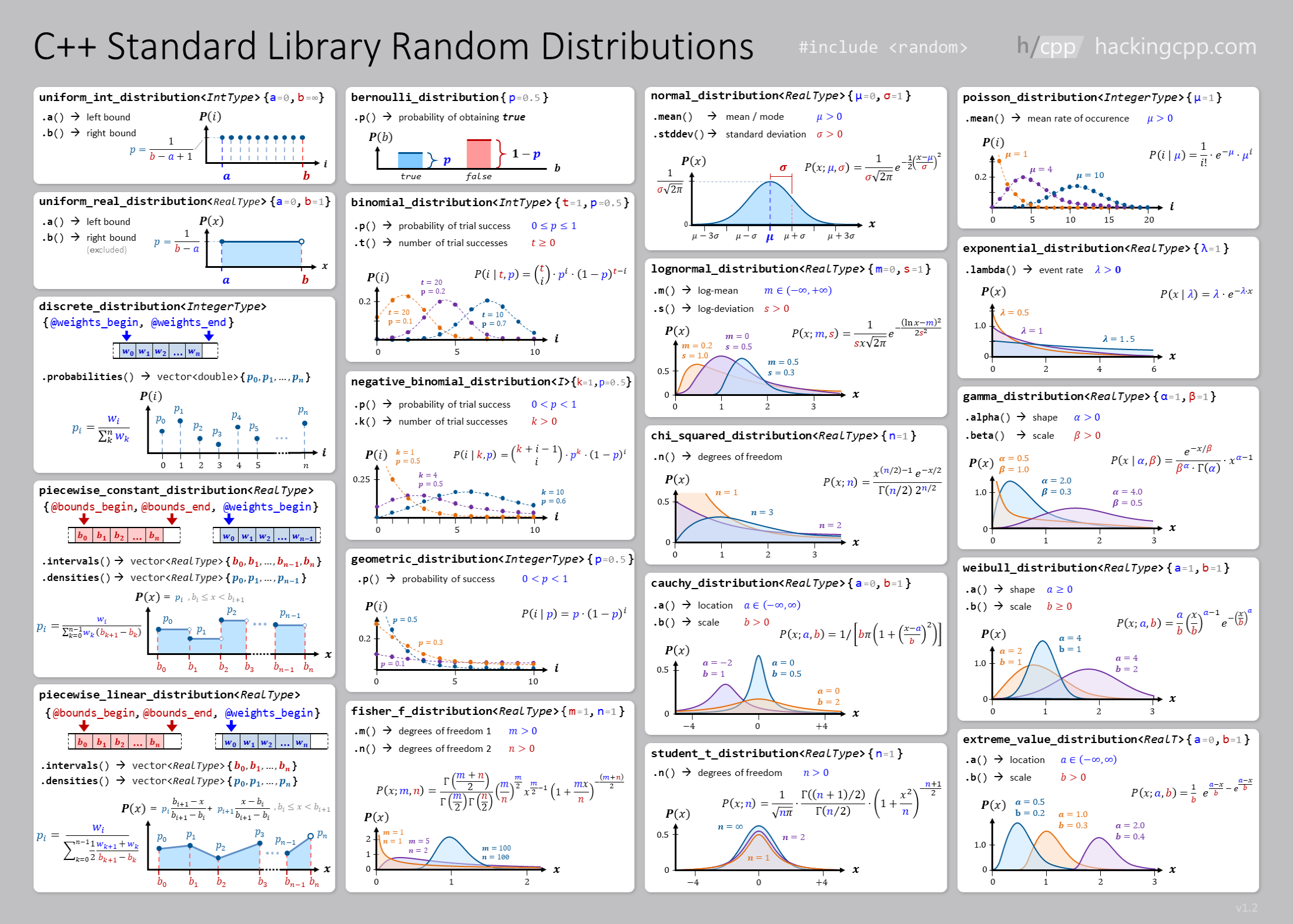
5.1.1. Uniform distribution with random seed#

From: "https://hackingcpp.com/cpp/std/random/uniform_real_distribution_plot.svg"

#include <random>
#include <iostream>

int main(void)
{
  //std::random_device rd; // inicializacion con semilla aleatoria
  //std::mt19937 gen(rd()); // genera bits aleatorios
  std::mt19937 gen(10); // fixed seed = 10
  std::uniform_real_distribution<> dis(1, 2); // distribucion
  for(int n = 0; n < 100; ++n) {
    std::cout << dis(gen) << std::endl;
  }
}

5.1.2. Uniform distribution controlled seed from command line#

#include <random>
#include <iostream>
#include <cstdlib>

int main(int argc, char **argv)
{
  const int seed = std::atoi(argv[1]);
  const int nsamples = std::atoi(argv[2]);
  std::mt19937 gen(seed);
  std::uniform_real_distribution<double> dis(1, 2);
  for(int n = 0; n < nsamples; ++n) {
    std::cout << dis(gen) << std::endl;
  }
  return 0;
}

Plot it.

5.1.3. Normal distribution controlled seed#

From: "https://hackingcpp.com/cpp/std/random/normal_distribution_plot.svg"

#include <random>
#include <iostream>

int main(void)
{
  int seed = 1;
  std::mt19937 gen(seed);
  std::normal_distribution<> dis{1.5, 0.3};
  for(int n = 0; n < 100000; ++n) {
    std::cout << dis(gen) << std::endl;
  }
}

5.1.4. Challenge#

Compute \(\pi\). How? Throw random numbers uniformly distributed in the unit square (randomly generate both \(x\) and \(y\) coordinates). Count how many fall inside the unit circle (\(N_c\)). The ratio of the later to the total random numbers \(N\) is a good approximation for the ratio of the circle area \(A_c = \pi/4\) over the total square area \(1\). In other words:

(5.1)#\[\begin{equation} \dfrac{N_c}{N} \simeq \dfrac{A_c}{A_s} = \frac{\pi}{4}, \end{equation}\]

therefore

(5.2)#\[\begin{equation} \pi \simeq 4\dfrac{N_c}{N}. \end{equation}\]

how much number do you need to get 2 decimals correctly? and for 6 decimals? compare with your peers to check who gets the most decimals correctly. How to make this faster?

#include <random>
#include <iostream>
#include <cstdlib>

double compute_pi(int seed, long nsamples);

int main(int argc, char **argv) 
{
  const int SEED = std::atoi(argv[1]);
  const long NSAMPLES = std::atol(argv[2]);
  std::cout.precision(16);
  std::cout.setf(std::ios::scientific);
  double mypi = compute_pi(SEED, NSAMPLES);
  std::cout << mypi << "\n"; 
    
  return 0;
}

double compute_pi(int seed, long nsamples) 
{
  // todo
}

5.1.5. Homework#

Create a histogram to compute the pdf and use it to test the random numbers produced by several distributions. Compute the pdf

5.2. Algorithms#

From: "https://hackingcpp.com/cpp/std/algorithms.png"

5.3. Containers#

https://hackingcpp.com/cpp/std/containers.html

5.3.1. Sequence containers#

From: "https://hackingcpp.com/cpp/std/sequence_containers.png"

5.3.1.1. Vector#

From: "https://hackingcpp.com/cpp/std/vector.png"

5.3.2. Associative containers#

From: "https://hackingcpp.com/cpp/std/associative_containers.png"

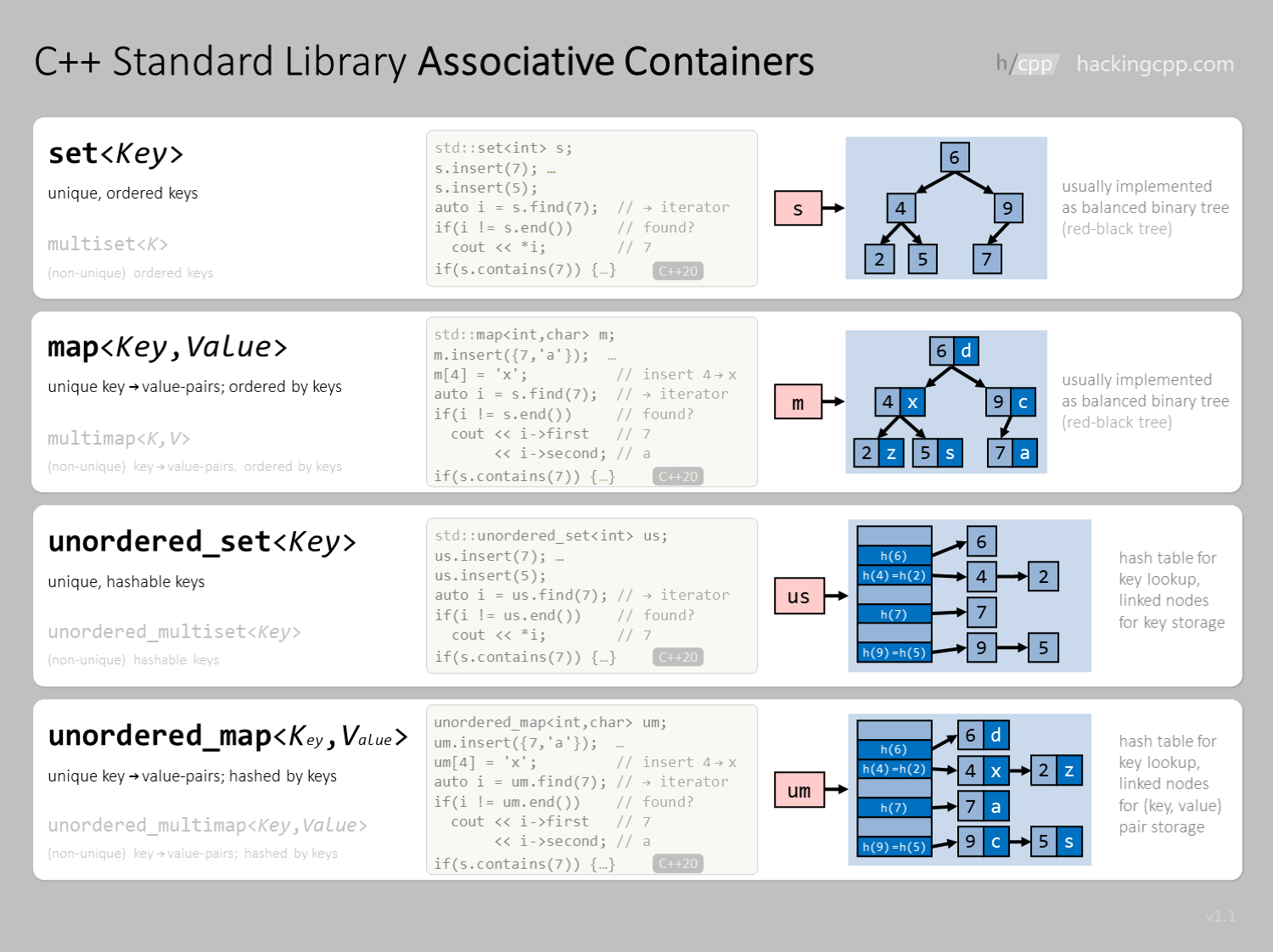
5.3.2.1. Map#

From: "https://hackingcpp.com/cpp/std/map.png"

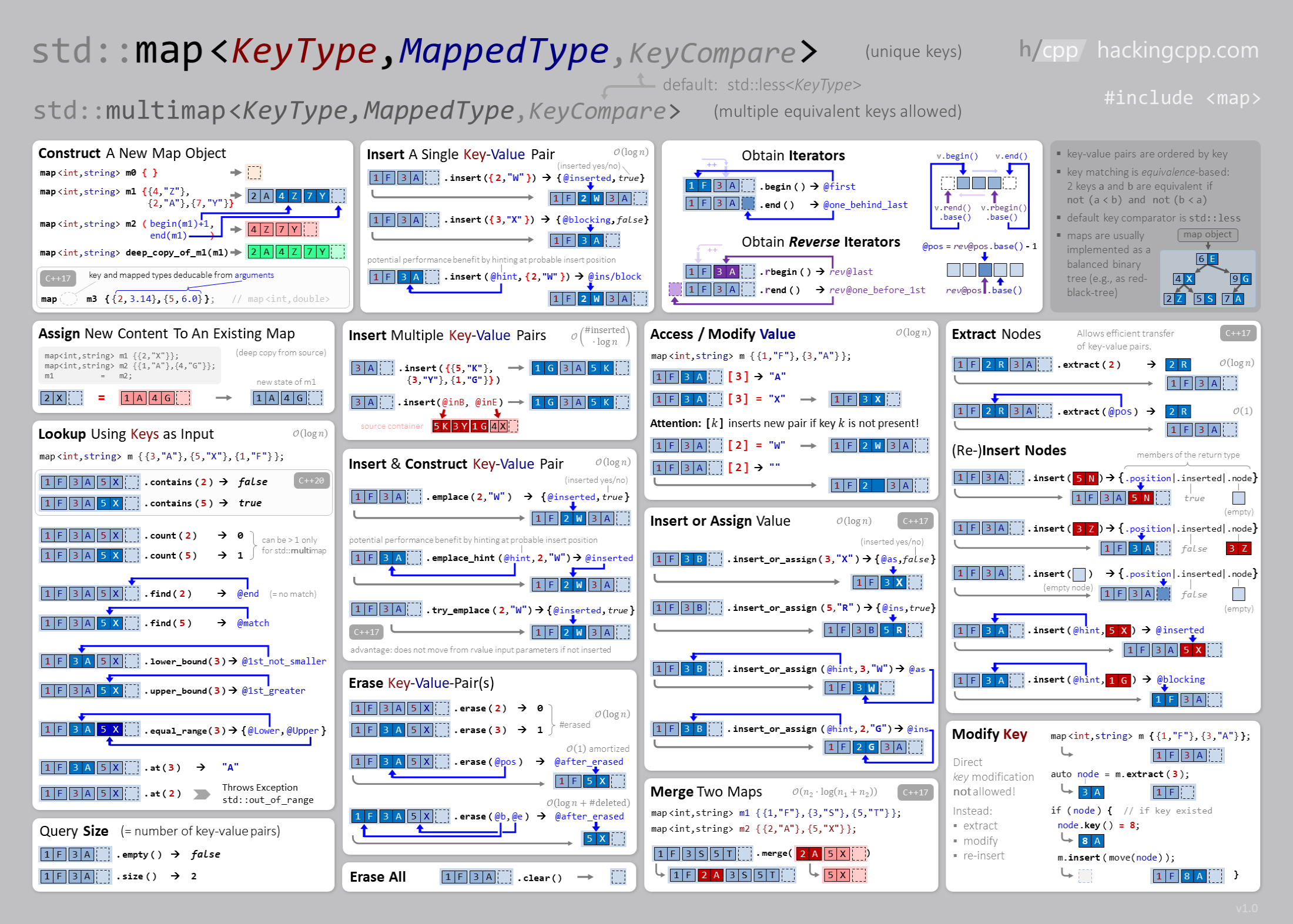
5.3.3. Challenge#

Here we are going to analyze texts from different authors to find a possible “signature”. We will compute the 20 most used words for a given book fr each author, and then plot it. To do so, let’s do the following:

Go to project Project Gutenberg. Search for: Jane Austen (e.g., Pride and Prejudice); Mark Twain (e.g., Huckleberry Finn). Download in plain text and strip headers/footers.
write a c++ program that reads the text name from the command line and, for each word in the given text:
- Convert it to lowercase (std::tolower).
- Remove basic punctuation (e.g., ,, ., ;, !, ?) from the end of words. (A simple check ispunct() on the last character can work for basics). Use the cleaned word as a key in a std::map<std::string, int>. Increment the corresponding integer value (histogram[word]++;).
The program should print to stdout the 20 most frequent words.
Plot the 20 most frequent words per author. Is there any difference? should some words be excluded?
What other measures do you think can be used to detect an authors “signature”?
Is it possible to infer the text genre?

Extra: Look at your friends histograms. Can you guess which book is?

#include <map>
#include <string>
#include <iostream>
#include <fstream>
#include <algorithm>
#include <numeric>
#include <set>

void analyze_document(const std::string & fname);

int main(int argc, char **argv)
{
    const std::string FNAME = argv[1];

    analyze_document(FNAME);

    return 0;
}

void analyze_document(const std::string & fname)
{
    std::ifstream file(fname);
    if (!file.is_open()) {
        std::cerr << "Error opening file: " << fname << std::endl;
        return;
    }

    std::map<std::string, int> word_count;
    std::string word;

    while (file >> word) {
        // todo
}

5.4. 🔬 Special functions in C++ (`<cmath>`, C++17+)#

Check https://en.cppreference.com/w/cpp/numeric/special_functions

This guide shows examples of interesting and useful special functions available in standard C++ using <cmath>. While the standard doesn’t cover all functions (like Bessel or Legendre), it includes many core tools needed for scientific computing and physics.

5.4.1. Gamma Function (`std::tgamma`)#

Purpose: Generalizes the factorial function
\(\Gamma(n) = (n-1)!\)

#include <iostream>
#include <cmath> // for std::tgamma

int main() {
    double val = 5.0;
    std::cout << "Gamma(" << val << ") = " << std::tgamma(val) << '\n'; // 24.0
}

Use case: Probability distributions, statistical physics, combinatorics

5.4.2. Log Gamma (`std::lgamma`)#

Purpose: Computes log(Gamma(x)) — numerically stable for large values

#include <iostream>
#include <cmath>

int main() {
    double x = 5.0;
    std::cout << "Log Gamma(" << x << ") = " << std::lgamma(x) << '\n'; // ~3.178
}

5.4.3. Error Function (`std::erf`, `std::erfc`)#

Purpose: Integral of the Gaussian function
Application: Diffusion, quantum mechanics, normal distribution CDF

#include <iostream>
#include <cmath>

int main() {
    double x = 1.0;
    std::cout << "erf(" << x << ") = " << std::erf(x) << '\n';
    std::cout << "erfc(" << x << ") = " << std::erfc(x) << '\n';
}

Wikipedia: Error function

5.4.4. Bessel Functions (via Boost)#

Note: Also in Use Boost.Math

#include <iostream>
#include <cmath>

int main() {
    double x = 2.5;
    std::cout << "J0(" << x << ") = " << std::cyl_bessel_j(0, x) << '\n';
}

#include <boost/math/special_functions/bessel.hpp>
#include <iostream>

int main() {
    double x = 2.5;
    std::cout << "J0(" << x << ") = " << boost::math::cyl_bessel_j(0, x) << '\n';
}

Use case: Wave equations, cylindrical geometries, optics

5.4.5. Legendre Polynomial#

#include <iostream>
#include <cmath>

int main() {
    double x = 0.5;
    std::cout << "P3(" << x << ") = " << std::legendre(3, x) << '\n';
}

5.4.6. Riemann Zeta#

#include <iostream>
#include <cmath>

int main() {
    std::cout << "Zeta(2) = " << std::riemann_zeta(2.0) << '\n'; // Should be π²/6
}

5.4.7. High-Precision Small-x Functions#

5.4.7.1. `std::expm1(x)` — Computes `exp(x) - 1` accurately for small `x`#

5.4.7.2. `std::log1p(x)` — Computes `log(1 + x)` accurately for small `x`#

#include <iostream>
#include <cmath>

int main() {
    double x = 1e-5;
    std::cout << "exp(x) - 1 = " << std::expm1(x) << '\n';
    std::cout << "log(1 + x) = " << std::log1p(x) << '\n';
}

5.5. Summary Table (C++ Standard)#

Function	C++ Function	Description
Gamma	`std::tgamma`	( \Gamma(x) )
Log-Gamma	`std::lgamma`	( \log(\Gamma(x)) )
Error Function	`std::erf`	Gaussian CDF integral
Complementary erf	`std::erfc`	( 1 - \text{erf}(x) )
exp(x)-1	`std::expm1`	More accurate near 0
log(1+x)	`std::log1p`	More accurate near 0

5.6. Advanced Special Functions (via external libraries)#

For advanced tools like:

Hermite
Zeta
Elliptic integrals

Use: