Common Numerical Integration Algorithms

Common Numerical Integration Algorithms#

Computing a numerical integral (or quadrature https://en.wikipedia.org/wiki/Numerical_integration?useskin=vector) is a typical problem that appears everywhere in numerical computing. The simple task of computing the error function, \(f(x) = \int_{0}^x e^{-t^2}\), requires the application of numerical techniques to calculate this (improper integral) over an arbitrary range.

In any numerical computing course you will start by exploring the trapezoidal and the simpsons rule. Here we are jus going to give the general formulation and then go directly to the functions given by scipy

Let’s compare several of the typical algorithms: https://www.geogebra.org/m/WsZgaJcc, and a beautiful visualization at https://www.youtube.com/watch?v=FnJqaIESC2s

All numerical quadratures can be written as

(3)#\[\begin{equation} \int_a^b dx\ f(x) \simeq \sum_i w_i f(x_i) dx + \epsilon, \end{equation}\]

where the weights \(w_i\) and the error \(\epsilon\) depend on the method chosen (see https://en.wikipedia.org/wiki/Newton–Cotes_formulas?useskin=vector).

Trapezoidal rule#

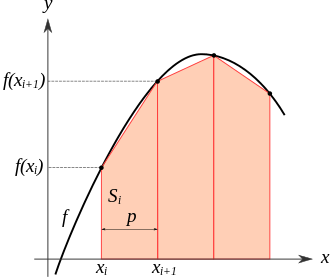
Here the function between two points is approximated by a straight line and the te area covered by the trapezoid is added up. See: https://en.wikipedia.org/wiki/Trapezoidal_rule

https://upload.wikimedia.org/wikipedia/commons/thumb/d/d1/Integration_num_trapezes_notation.svg/330px-Integration_num_trapezes_notation.svg.png

https://upload.wikimedia.org/wikipedia/commons/thumb/7/7e/Trapezium2.gif/330px-Trapezium2.gif

1-order interpolation

Better results for more intervals

Between two points, the integral is approximated as

(4)#\[\begin{equation} I (a, b) = \int_a^b dx \ f(x) \simeq \frac{b-a}{2} (f(a) + f(b)), \end{equation}\]

where the weights are \({1/2, 1/2}\).

The integral between two poins, \(a\) and \(b\), after dividing its lenght in \(N\) intervals (N+1 points, regular partition) of size \(\Delta x = \dfrac{b-a}{N}\), is given by

\[ \int_a^b f(x) dx \simeq \Delta x \left( \frac{f(x_0)}{2} + \sum_{k=1}^{N-1} f(x_k) +\frac{f(x_N)}{2}\right) + O(N^{-1}), \]

where \(x_k = x_0 + k \Delta x\), \(x_0 = a\), and \(x_N=b\).

Exercise#

Now, please create a function to compute the integral of a function (\(x^2\)) using the trapezoid algorithm.

OPTIONAL: Write the declaration and implementation on in integration.h and integration.cpp, respectively.

It must fulfill the following tests

std::cout << trapezoid(0.0, 1.0, 10, fun) << "\n";
std::cout << trapezoid(0.0, 1.0, 1000, fun) << "\n";
std::cout << trapezoid(0.0, 1.0, 10000000, fun) << "\n";

with results

0.3350000000000001
0.33333349999999995
0.33333333333333487

where fun is the square function.

Exercise#

Now use your implementation to compute the error function as a function of \(x\), using the partition shown. Your program must print also the relative error, comparing with the “exact” value from https://en.cppreference.com/w/cpp/numeric/math/erf . Print your data to erf_data.txt (print the x value, the numerical value of the integral, and the relative error)

(5)#\[\begin{equation} f(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2} dt \end{equation}\]

\(x \in [0, 10]\), \(\Delta x = 0.1\)

\(f(x=0), f(x=0+0.1), f(x=0+2\times 0.1), f(x=0+3\times 0.1), \ldots\)

You can use the following python script as a template script to plot the data

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np  
sns.set_context('poster')

x, erf, error = np.genfromtxt('erf_data.txt', unpack=True)
fig, ax = plt.subplots(1, 2)
ax[0].plot(x, erf, '-o', label="err function")
ax[0].legend()
ax[1].plot(x, error, '-s', label="relative error")
ax[1].legend()
ax[1].loglog()

# YOUR CODE HERE
raise NotImplementedError()

---------------------------------------------------------------------------
NotImplementedError                       Traceback (most recent call last)
Cell In[1], line 2
      1 # YOUR CODE HERE
----> 2 raise NotImplementedError()

NotImplementedError:

Simpsons rule#

In this case, the method uses three discrete points and approximate the function as a parabola (second order polynomial), to improve the numerical integral computation. See: https://en.wikipedia.org/wiki/Simpson%27s_rule

https://upload.wikimedia.org/wikipedia/commons/thumb/c/ca/Simpsons_method_illustration.svg/440px-Simpsons_method_illustration.svg.png

https://upload.wikimedia.org/wikipedia/commons/thumb/6/67/Simpsonsrule2.gif/440px-Simpsonsrule2.gif

2-order interpolation

Better results for more intervals

Between two points, the integral is

(6)#\[\begin{equation} I(a, b, 2) = \int_a^b dx\ f(x) \simeq \frac{b-a}{6} \left[ f(a) + 4f(\frac{a+b}{2}) + f(b)\right], \end{equation}\]

so the weights are \(\{1/6, 4/6, 1/6\}\).

Now, using a partition, you compute the integral as

(7)#\[\begin{equation} \int_a^b f(x) dx \simeq \frac{\Delta x}{3}\left( f(x_0) + 4 \sum_{k=1}^{N/2} f(x_{2k-1}) + 2\sum_{k=1}^{N/2-1} f(x_{2k}) + f(x_N)\right) + O(N^{-3}). \end{equation}\]

Notice that \(N\) must be even.

Now let’s implement it. Please add a new function to the integration.* files , that implements the simpsons rule.

std::cout << simpson(0.0, 1.0, 10) << "\n";

Should give

0.3333333333333333

Romberg method#

The Romberg Method applies Richardson extrapolation to the given integration technique. The implementation is completely analogous as for the derivatives case.

Implement it for the previous method shown and compare the errors as a function of \(N\), the number of intervals. Use the err function and fix \(x = 0.54432\).

Other techniques#

There are ways to improve the previous algorithms to decrease the error: using higher order decompositions, using Adaptative techniques, using Gaussian quadrature, mixing some of these techniques, etc. But implementing those methods by hand would be a daunting task.

NOTE: When you have tabular data, you will be almost forced to use either the trapezoid or the simpsons method. You could also first interpolate the data and then integrate.

Gaussian quadrature: Introduction to vectors#

Gaussian quadrature is a very clever technique that allows to compute integrals with a high precision and minimal number of points. First, notice that any numerical integral method can be written as

\[ I \simeq \sum w_i f(x_i), \]

where \(x_i\) are the evaluation points and \(w_i\) the associated weigths. What if you don’t fix the \(x_i\) to a uniform spacing, but, instead, try to compute both their optimal positions plus the optimal weights so you compute exactly the integral for an interpolating polynomial of degree \(2n-1\), using \(n\) points? that is the basic idea behind the method. The modern formulation, thanks to Jacobi, uses orthogonal polynomials, usually in the [-1, 1] domain (so you need to re-scale your data).

Image Description
From: "https://upload.wikimedia.org/wikipedia/commons/thumb/9/93/Comparison_Gaussquad_trapezoidal.svg/660px-Comparison_Gaussquad_trapezoidal.svg.png"
In this image, it is illustrated that although the Gaussian method uses only two points, it is exact since the integration is done on a 3-degree polynomial.

For the Gauss-Legendre formulation, you can check the weights at https://en.wikipedia.org/wiki/Gaussian_quadrature?useskin=vector#Gauss%E2%80%93Legendre_quadrature

To succesfully apply the Gaussian quadrature technique to a general integral on the interval [a, b], we need to map it to the interval [-1, 1], so we can use the mapping

\[ x = \frac{b-a}{2}x' + \frac{b+a}{2}, \]

therefore

\[ \int_a^b f(x) dx \simeq \frac{b-a}{2} \sum w_i f\left(\frac{b-a}{2}x' + \frac{b+a}{2}\right) \]

using the \(w_i\) from the method.

Example using a vector to store the weights.#

For an increasing number of points, you will need to use many variables to store the weights. For a degree \(n=5\), you will need five variables to store the weights, five more for the points, and then manually process that. It will be much better to store them in an data structure that allow us to handle the operations in a generic way. In this case, it will be a std::vector, which allows us to store data, contiguously in memory, and process it using simple for loops (SIMD).

Our declaration could be

double gauss_5(double a, double b, fptr fun);

and its implementation (you need to finish it)

double gauss_5(double a, double b, fptr fun)
{
    std::vector<double> x(5); // store five points in the array
    std::vector<double> w(5); // store five weights in the array
    // initialize the data, sorted from left to right
    x[0] = -std::sqrt(5 + 2std::sqrt(10/7));
    x[1] = -std::sqrt(5 - 2std::sqrt(10/7));
    x[2] = 0.0;
    // ...
    w[0] = (322 - 13*std::sqrt(70))/(900);
    w[1] = (322 + 13*std::sqrt(70))/(900);
    w[2] = 128.0/255.0;
    //...
    // compute the integral
    double result = 0.0;
    for (int ii = 0; ii < 5; ++ii) {
        result += w[ii]*fun((b-a)*x[ii]/2 + (b+a)/2);
    }
    return result*???;
}

Notice how easy is to process data in an array.

Now finish the implementation, and print the error, as a function of \(x\), computing the err function, comparing the relative errors with trapezoid, simpson, trapezoid+richardson, simpson+trapezoid, gauss_5. Plot it.

Exercises#

Gauss quadrature of order 7#

(REF: Sirca, Computational Methods in Physics. Also https://en.wikipedia.org/wiki/Gaussian_quadrature) The Gaussian quadrature is a very powerful method to compute integrals, where the points and weights are wisely chosen to improve the algorithm precision. The method is formulated in the range [-1, 1], so maybe the general integral must be scaled as

(8)#\[\begin{equation} \int_a^b f(x) dx = \frac{b-a}{2} \sum_{j=1}^{n} w_j f\left(\frac{b-a}{2} x_j + \frac{a+b}{2} \right) + O((b-a)^{2n+1}). \end{equation}\]

The next table shows the points positions and weights for the Gaussian integral of order 7, \(G_7\),

Nodes position Weigths
$\pm 0.949107912342759$ 0.129484966168870
\(\pm 0.741531185599394\) 0.279705391489277
\(\pm 0.405845151377397\) 0.381830050505119
$0.000000000000000$ 0.417959183673469

  1. Implement the \(G_7\) method (a functor would be useful) and compare its result with the exact one. Integrate the function \(\sin\sqrt x\) on the interval \([2, 8.7]\). The exact indefinite integral is \(2\sin\sqrt x - 2\sqrt x\cos\sqrt x\).

    G7: 4.637955250321647
    Exact: 4.637955200036554

  2. Compute the err function as a function of \(x \in [0, 10.0]\) in steps of \(0.05\), using both \(G_7\) and Simpson+Richardson and plot the relative difference with the “exact” function std::erf (https://en.cppreference.com/w/cpp/numeric/math/erf).

For more coefficients and higer orders, see https://pomax.github.io/bezierinfo/legendre-gauss.html

Integrating a datafile#

The following data (file accel.txt) represents the acceleration of a car as a function of time

0.5 2
1 3
1.3 3.6
1.7 4.4
1.9 4.15
2.1 3.85
2.5 3.25
2.9 2.65

Save the data into the corresponding file. Then write a program to read the data and compute the velocity as a function of time by integrating at each time step.

Cumulative probability#

The probability density function for the Gamma distribution is

(9)#\[\begin{equation} f(x; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha) x^{\alpha -1} e^{-\beta x} }, \end{equation}\]

para \(0 < x < \infty\). Compute and plot the cumulative density function, using both the simpson method and the gaussian \(g_7\), defined as

(10)#\[\begin{equation} F(x; \alpha, \beta) = \int_0^x dt f(t; \alpha, \beta), \end{equation}\]

for \(x \in [0.0, 20.0]\), with \(\alpha = 7.5, \beta = 1.0\).

Di-logarithm function#

The di-logarithm function is defined as

(11)#\[\begin{equation} \mathrm{Li}_2(x) = -\int_0^x \frac{\ln(1-t)}{t} dt. \end{equation}\]

Plot the di-logarithm function for \(x \in (0.0, 1.0)\). If you use simpson, always make sure that the error is less than \(10^{-6}\). You might need to transform the variable and/or split the integral to avoid numerical problems.

Moment distribution#

The kth moment for a probability distribution is

(12)#\[\begin{equation} \lt x^k \gt = \int x^k f(x) dx, \end{equation}\]

Compute the first ten moments for the Gamma distribution ,

(13)#\[\begin{equation} f(x; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha) x^{\alpha -1} e^{-\beta x} }. \end{equation}\]

Arch lenght, mass, centroid#

The arc length of a curve \(y(x)\) is given by

(14)#\[\begin{equation} s = \int_a^b dx \sqrt{1 + \left(\frac{dy}{dx} \right)^2}. \end{equation}\]

If a linear body has a density \(\rho(x)\), the total mass would be

(15)#\[\begin{equation} M = \int \rho(x) ds. \end{equation}\]

The \(x\) position of the centroid can also be computed as

(16)#\[\begin{equation} \overline x = \frac{\int x\rho ds}{\int \rho ds} \end{equation}\]

  1. (Boas, Mathematical Physics) Compute the arch length for the catenary \(y = \cosh x\) between \(x=-1\) and \(x=1\).

  2. For a chain with shape \(x^2\), with density \(|x|\), between \(x = -1\) and \(x=1\), compute

    1. The arc length

    2. The total mass \(M\)

    3. \(\overline x\)

    4. \(\overline y\)