Vector operations: Coefficient-wise , array computing#
Coefficient-wise operations, like the vector sum (which operate component by
component), are very common and useful. For instance, the whole numpy library
is based on that (https://numpy.org/doc/stable/user/basics.broadcasting.html).
In c++ you can also do it, and it simplifies a lot many operations related to
vectors. You have two options: using the standard library valarray, or using
Eigen array.
This is, for instance, what you would like to have when adding two structures representing vectors:
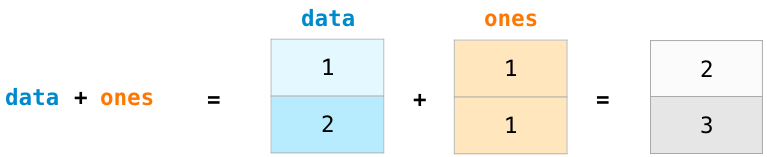
or with more operations
or with scalars,
Function evaluation#
Furthermore , mathematical function evaluated in this array computing approach means evaluating the function on each component, such as
means
C++ valarray#
You can find the reference implementation at https://en.cppreference.com/w/cpp/numeric/valarray .
#include <iostream>
#include <valarray>
#include <cmath>
int main()
{
std::valarray<int> v = {1,2,3,4,5,6,7,8,9,10};
double suma = v.sum();
std::cout << suma << "\n";
return 0;
}
Example: Using apply#
Cómo usar la utilidad apply para multiplicar todos los elementos por 2 si el numero es impar y por 3 si el numero es par? Piense en la solución usando for e if y luego puede mirar a https://en.cppreference.com/w/cpp/numeric/valarray/apply
Indexing#
A simple example for indexing, is the following (https://en.cppreference.com/w/cpp/numeric/valarray/operator%3D)
#include <iomanip>
#include <iostream>
#include <valarray>
void print(const char* rem, const std::valarray<int>& v)
{
std::cout << std::left << std::setw(36) << rem << std::right;
for (int n: v) std::cout << std::setw(3) << n;
std::cout << '\n';
}
int main()
{
std::valarray<int> v1(3);
v1 = -1; // (3) from a scalar
print("assigned from scalar: ", v1);
v1 = {1, 2, 3, 4, 5, 6}; // (8): from initializer list of different size
print("assigned from initializer_list:", v1);
std::valarray<int> v2(3);
v2 = v1[std::slice(0,3,2)]; // (4): from slice array
print("every 2nd element starting at pos 0:", v2);
v2 = v1[v1 % 2 == 0]; // (6): from mask array
print("values that are even:", v2);
std::valarray<std::size_t> idx = {0,1,2,4}; // index array
v2.resize(4); // sizes must match when assigning from gen subscript
v2 = v1[idx]; // (7): from indirect array
print("values at positions 0, 1, 2, 4:", v2);
return 0;
}
Masks#
As you can see, all operations are done at the element level. You can also define masks:
#include <iostream>
#include <valarray>
int main()
{
std::valarray<int> data = {0,1,2,3,4,5,6,7,8,9};
std::cout << "Initial valarray: ";
for(int n: data) std::cout << n << ' ';
std::cout << '\n';
data[data > 5] = -1; // valarray<bool> overload of operator[]
// the type of data>5 is std::valarray<bool>
// the type of data[data>5] is std::mask_array<int>
std::cout << "After v[v>5]=-1: ";
for(std::size_t n = 0; n < data.size(); ++n)
std::cout << data[n] << ' '; // regular operator[]
std::cout << '\n';
}
There is also a nice utility, apply, that you can use to apply a function to
each element:
#include <iostream>
#include <valarray>
#include <cmath>
int main()
{
std::valarray<int> v = {1,2,3,4,5,6,7,8,9,10};
v = v.apply([](int n)->int {
return std::round(std::tgamma(n+1));
});
for(auto n : v) {
std::cout << n << ' ';
}
std::cout << '\n';
}
Exercises#
Dot product#
Create a program that computes the dot product among two math vectors using valarray. Your program must read the vector size from the command line. Fill them using any function you want.
Heap or stack?#
Is a valarray in the heap or the stack? Verify (check https://en.cppreference.com/w/cpp/numeric/valarray/resize)
Filter data#
Using the overloaded operators create a valarray for N=1000 points between 0 and \(2\pi\), then compute the \(\sin\) of those numbers and assing the result to a another valarray, and finally print only the values that fulfill that \(|\sin x| \le 0.5\). All of this without using loops.
Simulation#
If you discretize time in steps of size \(\delta t\), and you have the forces on a given ideal particle, you can compute the next position using the Euler algorithm,
Use valarrays to model the vectors. Compute the trayectory of a particle of mass \(m=0.987\), with initial conditions \(\vec R(0) = (0, 0, 4.3), V(0) = (0.123, 0.0, 0.98)\), under the influence of gravity. Plot it. Later add some damping. Later add some interaction with the ground.
Extract odd values#
Fill an std::valarray with random integers numbers uniformly distributed in [1000, 2500], and then extract the even values and compute their mean.
Cross product#
Implement a function to compute the cross product between two 3d vectors. Using it, implement a function to compute the angle between the vectors. Remember that
Check test cases like \(\vec A \times \vec A = \vec 0, \hat i \times \hat j = \hat k, \ldots\)
Perpendicular vector#
Use the previous cross product function to find a unit vector perpendicular to two vectors.
Plane equation#
Find the equation of the plane in the form \(ax + by + cz + d = 0\), saving the result in a 4d std::vector, given three 3D points represented using std::valarray.
Vector product#
Write a function that returns the vector product
Classical angular momentum and centripetal acceleration#
Given a mass \(m\), a position \(\vec r\), and a velocity \(\vec v = \omega \times \vec r \), compute both the angular momentum \(\vec L = m \vec r \times (\vec r \times \vec \omega)\) and the centripetal acceleration \(\vec a = \vec \omega \times (\vec \omega \times \vec r)\), using two different functions
Other libraries#
Eigen arrays: coefficient wise computation#
This library also implements element-wise operations and data structs, https://eigen.tuxfamily.org/dox/group__TutorialArrayClass.html , https://eigen.tuxfamily.org/dox/group__QuickRefPage.html#title6 . There are many overloaded operations that you can use. Plase check the docs.
This is an example of a sum, element-wise
#include <eigen3/Eigen/Dense>
#include <iostream>
int main()
{
Eigen::ArrayXXf a(3,3);
Eigen::ArrayXXf b(3,3);
a << 1,2,3,
4,5,6,
7,8,9;
b << 1,2,3,
1,2,3,
1,2,3;
// Adding two arrays
std::cout << "a + b = " << std::endl << a + b << std::endl << std::endl;
// Subtracting a scalar from an array
std::cout << "a - 2 = " << std::endl << a - 2 << std::endl;
}
and this an example for vector product
#include <eigen3/Eigen/Dense>
#include <iostream>
int main()
{
Eigen::ArrayXXf a(2,2);
Eigen::ArrayXXf b(2,2);
a << 1,2,
3,4;
b << 5,6,
7,8;
std::cout << "a * b = " << std::endl << a * b << std::endl;
}
More operations:
#include <eigen3/Eigen/Dense>
#include <iostream>
int main()
{
Eigen::ArrayXf a = Eigen::ArrayXf::Random(5);
a *= 2;
std::cout << "a =" << std::endl
<< a << std::endl;
std::cout << "a.abs() =" << std::endl
<< a.abs() << std::endl;
std::cout << "a.abs().sqrt() =" << std::endl
<< a.abs().sqrt() << std::endl;
std::cout << "a.min(a.abs().sqrt()) =" << std::endl
<< a.min(a.abs().sqrt()) << std::endl;
}